
只要网络足够宽,深度学习动态就能大大简化,并且更易于理解。
最近的许多研究结果表明,无限宽度的DNN会收敛成一类更为简单的模型,称为高斯过程(Gaussian processes)。
于是,复杂的现象可以被归结为简单的线性代数方程,以了解AI到底是怎样工作的。
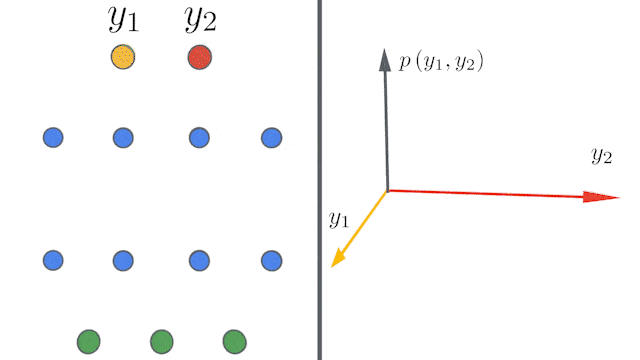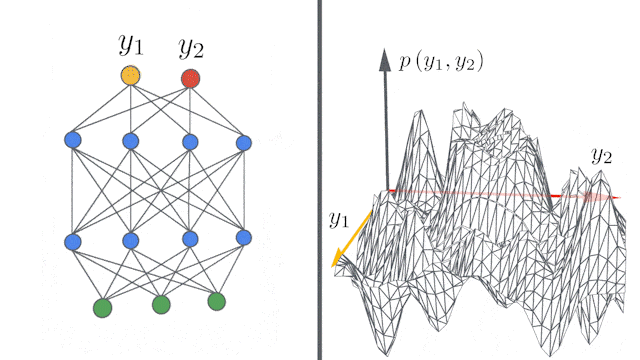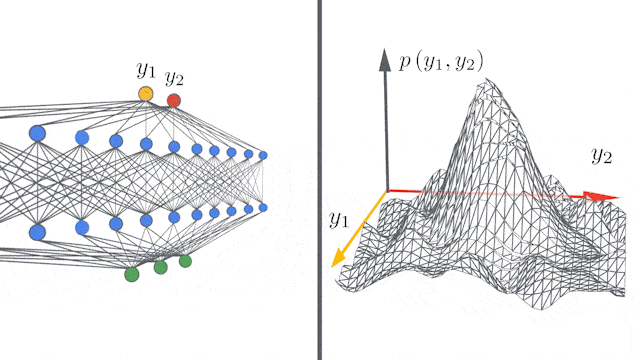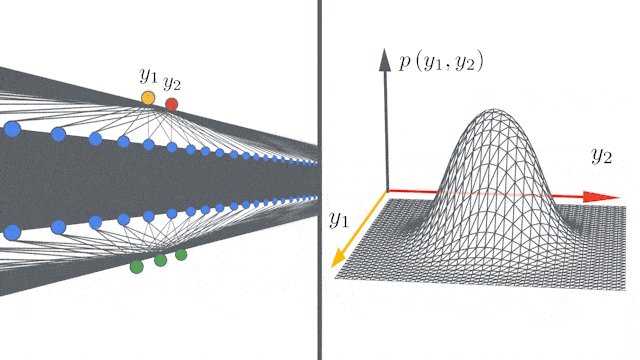
所谓的无限宽度(infinite width),指的是完全连接层中的隐藏单元数,或卷积层中的通道数量有无穷多。
但是,问题来了:推导有限网络的无限宽度限制需要大量的数学知识,并且必须针对不同研究的体系结构分别进行计算。对工程技术水平的要求也很高。
谷歌最新开源的 Neural Tangents,旨在解决这个问题,让研究人员能够轻松建立、训练无限宽神经网络。
甚至只需要5行代码,就能够打造一个无限宽神经网络模型。
这一研究成果已经中了ICLR 2020。戳进文末Colab链接,即可在线试玩。
开箱即用,5行代码打造无限宽神经网络模型
Neural Tangents 是一个高级神经网络 API,可用于指定复杂、分层的神经网络,在 CPU/GPU/TPU 上开箱即用。
该库用 JAX编写,既可以构建有限宽度神经网络,亦可轻松创建和训练无限宽度神经网络。
有什么用呢?举个例子,你需要训练一个完全连接神经网络。通常,神经网络是随机初始化的,然后采用梯度下降进行训练。
研究人员通过对一组神经网络中不同成员的预测取均值,来提升模型的性能。另外,每个成员预测中的方差可以用来估计不确定性。
如此一来,就需要大量的计算预算。
但当神经网络变得无限宽时,网络集合就可以用高斯过程来描述,其均值和方差可以在整个训练过程中进行计算。
而使用 Neural Tangents ,仅需5行代码,就能完成对无限宽网络集合的构造和训练。
from neural_tangents import predict, stax
init_fn, apply_fn, kernel_fn = stax.serial(
stax.Dense(2048, W_std=1.5, b_std=0.05), stax.Erf(),
stax.Dense(2048, W_std=1.5, b_std=0.05), stax.Erf(),
stax.Dense(1, W_std=1.5, b_std=0.05))
y_mean, y_var = predict.gp_inference(kernel_fn, x_train, y_train, x_test, ‘ntk’, diag_reg=1e-4, compute_cov=True)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
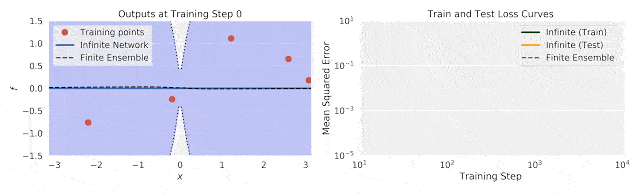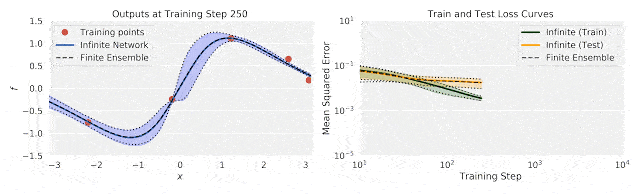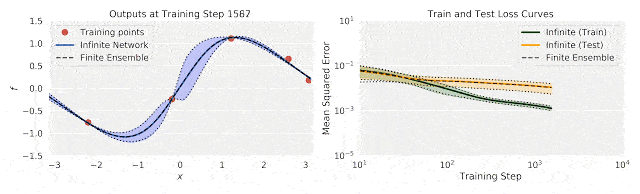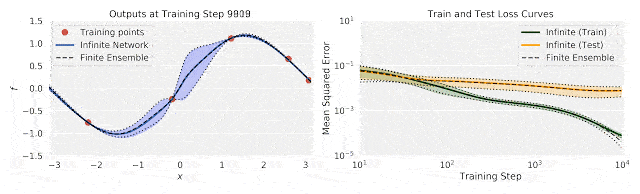
上图中,左图为训练过程中输出(f)随输入数据(x)的变化;右图为训练过程中的不确定性训练、测试损失。
将有限神经网络的集合训练和相同体系结构的无限宽度神经网络集合进行比较,研究人员发现,使用无限宽模型的精确推理,与使用梯度下降训练整体模型的结果之间,具有良好的一致性。
这说明了无限宽神经网络捕捉训练动态的能力。
不仅如此,常规神经网络可以解决的问题,Neural Tangents 构建的网络亦不在话下。
研究人员在 CIFAR-10 数据集的图像识别任务上比较了 3 种不同架构的无限宽神经网络。
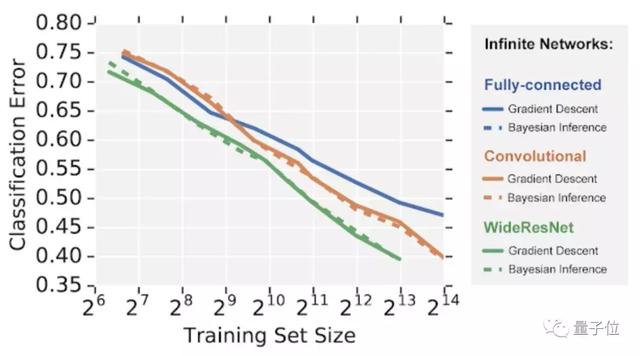
可以看到,无限宽网络模拟有限神经网络,遵循相似的性能层次结构,其全连接网络的性能比卷积网络差,而卷积网络的性能又比宽残余网络差。
但是,与常规训练不同,这些模型的学习动力在封闭形式下是易于控制的,也就是说,可以用前所未有的视角去观察其行为。
对于深入理解机器学习机制来说,该研究也提供了一种新思路。谷歌表示,这将有助于“打开机器学习的黑匣子”。
传送门
论文地址:https://arxiv.org/abs/1912.02803
谷歌博客:https://ai.googleblog.com/2020/03/fast-and-easy-infinitely-wide-networks.html
GitHub地址:https://github.com/google/neural-tangents
Colab地址:https://colab.research.google.com/github/google/neural-tangents/blob/master/notebooks/neural_tangents_cookbook.ipynb