深圳幻海软件技术有限公司 欢迎您！
更多

【数据结构与算法】设计循环队列

2023-03-28

队列 obj rear
文章目录👑前言如何设计循环队列设计循环队列整体的代码📯写在最后👑前言🚩前面我们用队列实现了一个栈，用栈实现了一个队列，相信大家随随便便轻松拿捏，而本章将带大家上点难度，我们来设计一个循环队列。🚩对于循环队列，重点就在一个“循环”，意思也就是该队列首尾相连形成一个环，但其本质还是不变，队列先

文章目录

  • 👑前言
  • 如何设计循环队列
  • 设计循环队列
  • 整体的代码
  • 📯写在最后

👑前言

🚩前面我们 用队列实现了一个栈 ，用栈实现了一个队列 ，相信大家随随便便轻松拿捏，而本章将带大家上点难度，我们来 设计一个循环队列。
🚩对于循环队列，重点就在一个 “ 循环 ”，意思也就是该队列首尾相连形成一个环，但其本质还是不变，队列 先进先出 的性质依旧存在，只不过环的大小有限定（限定放多少数据就只能放多少数据）。
🚩那么我们如何来设计这样的一个环，使它既能够像队列一样，又可以体现循环的性质？下面就带大家探讨一波。

如何设计循环队列

  • 那么该如何设计一个循环队列呢？首先第一步当然就是选取一个存储结构来存放数据，是选顺序表的数组呢还是链表呢？

  • 我们先来看看对循环队列的介绍：循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

由以上所说，既然是队尾被连接在队首之后形成一个循环，并且之前我们讲解的队列是选用的链式储存结构，那我们第一个想到的就是选用链式的储存结构来存储数据，因为只要链表的尾节点的next指向头节点就形成了循环，这是很容易想到的。那我们就先对链式这一储存结构进行分析，看到底合不合适。

抽象图：

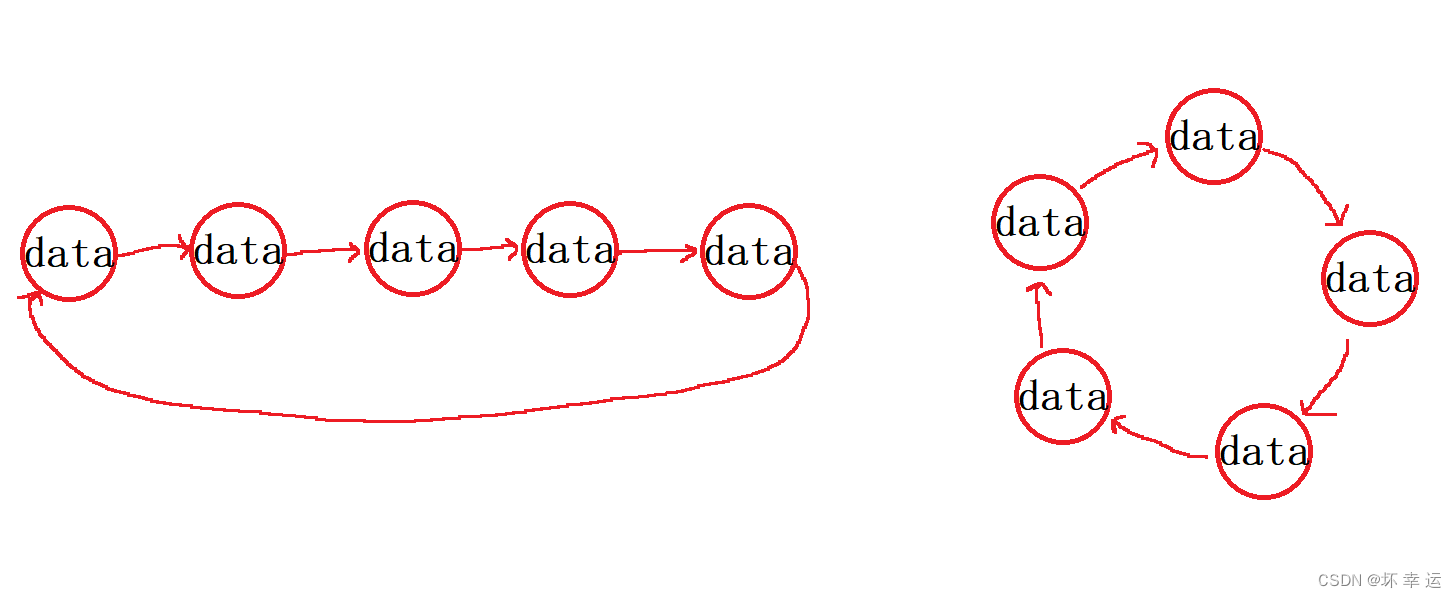
  • 既然是队列，那就需要两个指针，一个命名为front指向头，一个命名为rear指向尾。由于是循环队列，刚开始就将空间开好（固定长度），那么此时front和rear都指向同一个节点，如下：

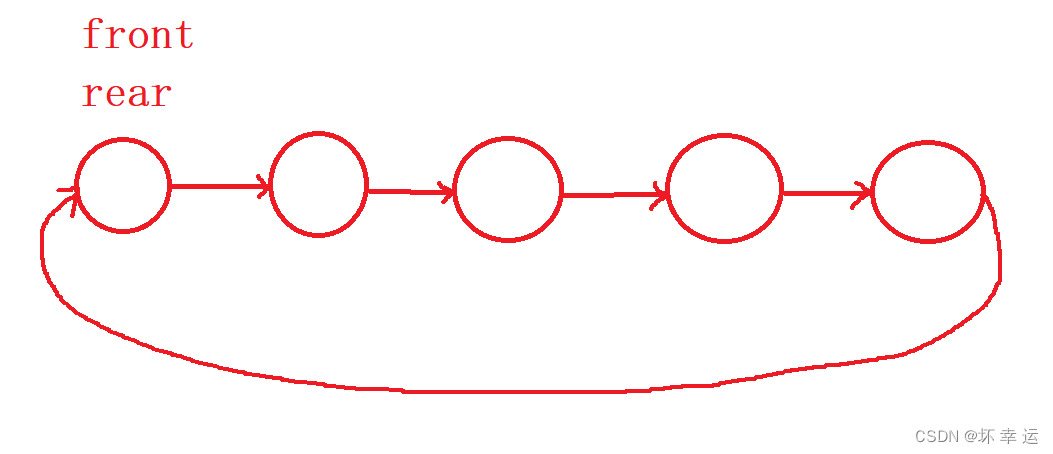
  • 那么此时入队列的操作过程如下：

  • 可以看到，rear指向有效数据节点的下一个位置。当队列入满的时候，rear指针此时又与front指针相等了，我们再来看看出队列的过程（出队列数据可以不用抹去，访问不到）：

  • 由上面的两个操作我们不难发现，当队列为空的时候，front指针与rear指针相等，当队列满的时候，front指针与rear指针也相等，这不免就会出现冲突问题：判空和判满将如何判断呢？

  • 这里有两种方案：

    1. 第一个是多创建一个变量来统计数据的个数，当判空和判满的时候根据这个变量就可以实现；
    2. 第二个是多开一个空间（注意不是哨兵位节点），也就是规定长度为多少，开空间的时候开长度加一个空间，如下图：


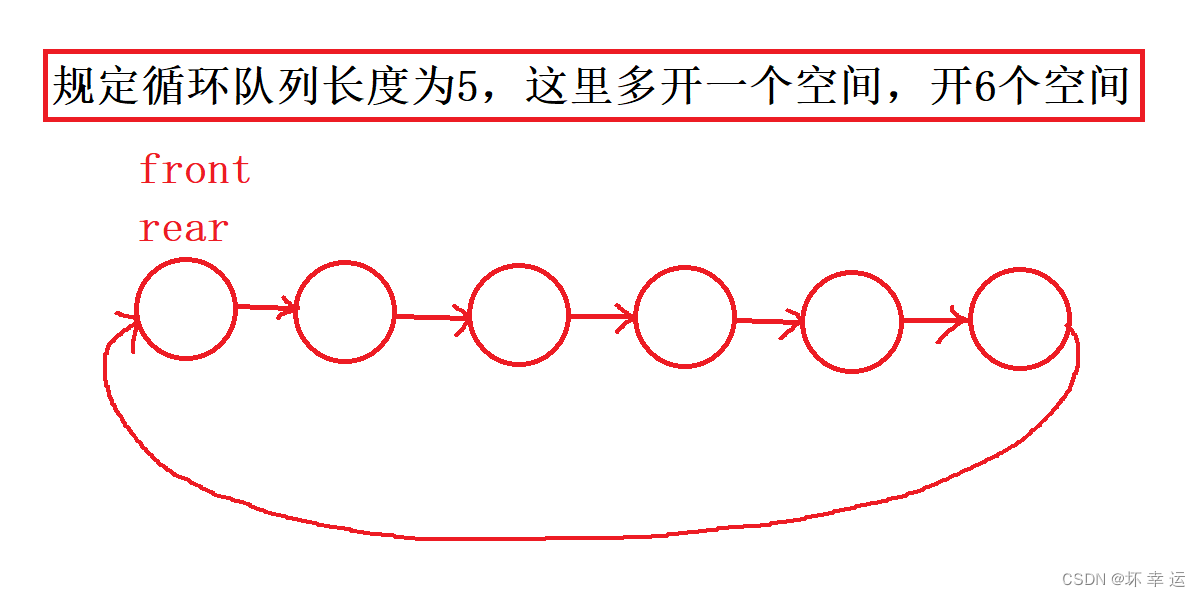
可以看到，方案二当循环队列为空的时候，front == rear，当循环队列为满的时候，如下图：


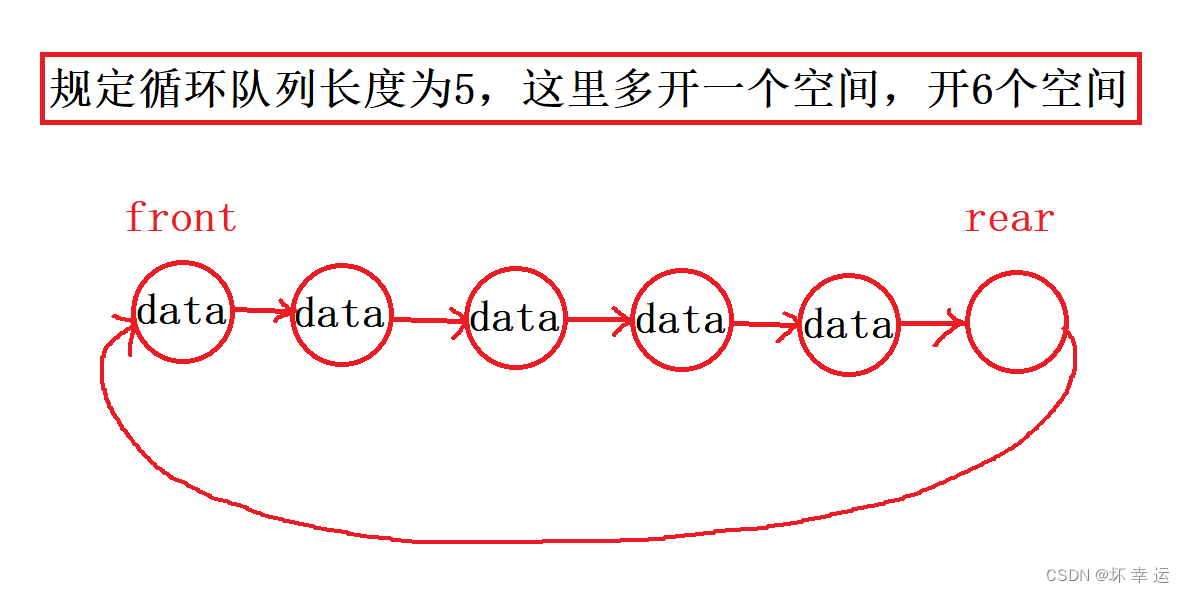
由此图不难得出，当循环队列为满时，有rear->next == front，所以，方案二对于判空和判满的区分也是挺不错的。不过，大家有没有观察到，对于链式储存结构，无论是方案一还是方案二，都不好找队尾数据，因为它处在rear指针的前一个节点，实在是要找的话，就需要遍历一遍循环队列，或者在一开始就另外再定义一个prev指针，指向rear指针的前一个节点，这些都是比较麻烦的。那么根据此问题，由于数组存储形式支持随机访问，所以下面我们再来看看数组的存储形式怎么样。

  • 对于数组的存储形式，整体上来说与链式存储形式差不太多。由于循环队列的长度是固定的，因此数组的存储形式抛弃了扩容这一弱点。

数组存储形式图：

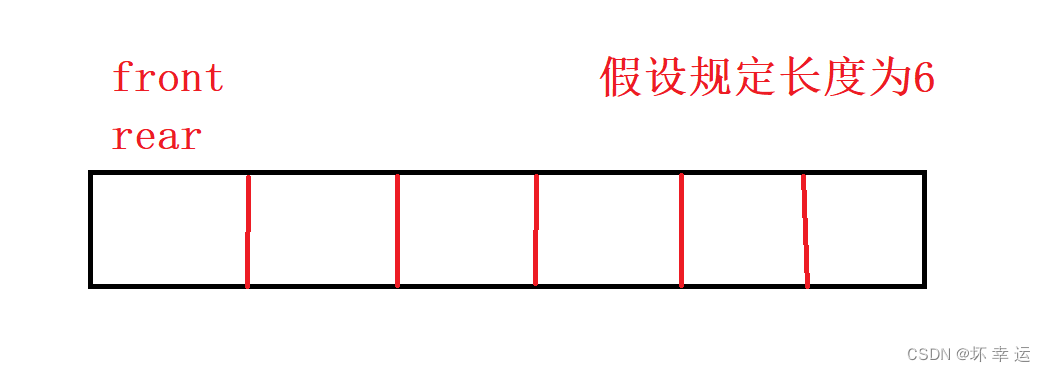
  • 有了链式存储的分析判断，不难得出，上图的数组存储形式也会出现判空和判满实现的冲突问题。因此这里也需要解决方案，而数组存储形式的解决方案与链式存储形式的解决方案是相同的，无非就是多定义一个变量来统计数据的个数，或者多开一个空间。多定义一个变量来统计数据的个数固然可以实现，但这里我们选取多开一个空间的形式来进行分析。

如果是多开一个空间，那么当循环队列满时，有以下情况：


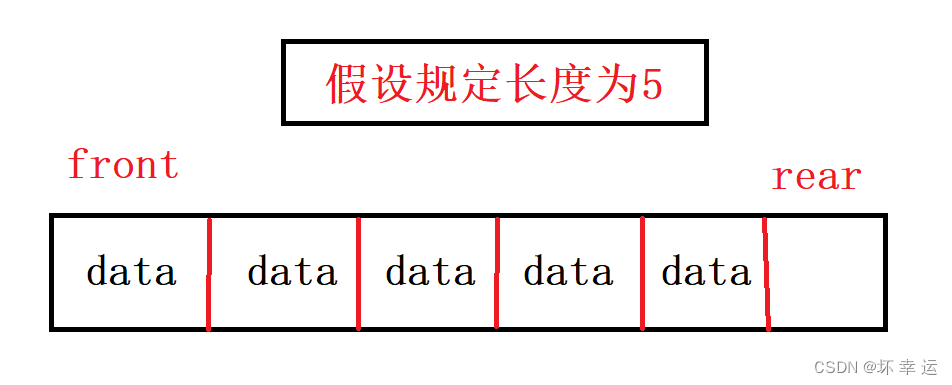
2.

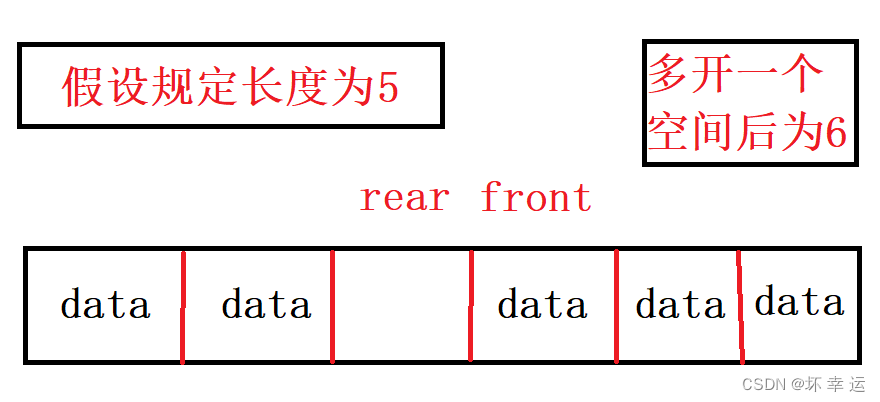
(注意：front与rear两个指针分别是对应数据的下标 | 设规定的长度为k)

  • 如果是2情况，判满可以判断 rear + 1 == front ？ ，但还有1情况rear + 1不会等于front，并且会超出数组的下标范围，因此这里可以对rear + 1取模，也就是判断 (rear + 1) % (k + 1) == front ? 即可。有了这种判断方式，无论rear是否指向数组的最后一个位置，他都可以判断，因为：当rear不是指向数组的尾时，它加一模上一个(k + 1)完全不会受到影响，就相当于是判断 rear + 1 == front ？ 一样。而rear指向数组的尾时，这样操作最终就是判断 front == 0 ？ 一样。

  • 那数组的判满解决了，判空如何呢？其实判空很简单，只需要判断rear是否等于front即可。

由于是数组存储形式，因此支持下标的随机访问，所以这里获取队头和队尾元素都非常的方便。

  • 如果是获取队头元素，直接返回front指向的数据即可；如果是获取队尾元素，只需要返回rear的前一个位置的数据即可，但是，如果rear此时指向数组的开头又该怎么找队尾元素呢?

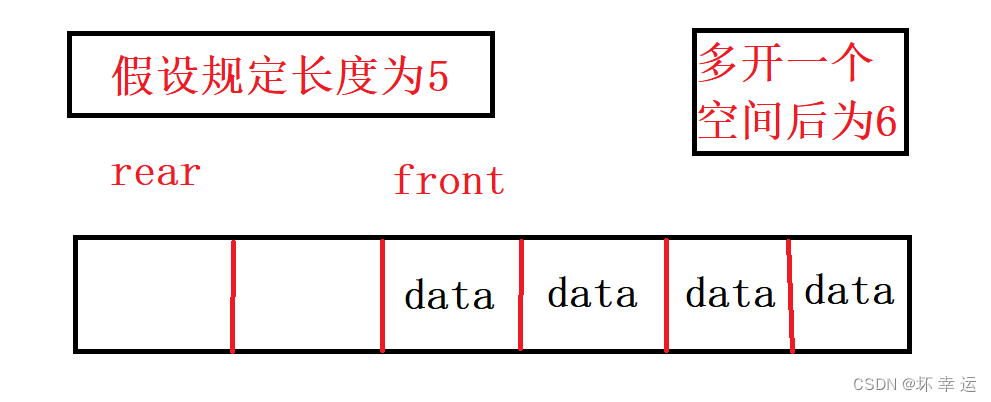
  • 这里我们将 rear + k 然后模上 k + 1 即可。因为，如果rear是指向数组开头，rear加上k后刚好指向数组的最后一个位置，也就是循环队列的队尾。如果rear不是指向数组开头， (rear + k) % (k + 1) 刚好是rear的前一个位置，所以，这样的取模的方式，完美的实现了取队尾的功能。

综上来看，链式储存结构与数组储存结构还是数组储存结构更胜一筹，因为在取队尾元素这一块数组储存结构碾压链式储存结构，所以，这里我们选择数组储存结构来实现循环队列。

  • 这里我们采用多开一个空间的方式来实现。

  • 确定了以数组存储结构来存储数据后，那么该如何实现数据的入队和出队呢？

首先来看看数据入队列示意图：


  • 对于第一张图的入队列，就是在当前rear位置插入，然后rear加加即可。但是对于第二张图，rear在最后位置的时候插入数据，此时rear加加就超过数组的长度了，因此我们每次在rear加加后需要执行一下 rear %= (k + 1) 这条语句，这样做，rear在数组的尾插入数据时，会将rear转算成0，也就是指向数组的开头位置，如果rear不在数组的尾插入数据，此时rear的位置不会受任何的影响。

然后再来看看数据出队列示意图：

  • 对于第一张图，每次删除其实只需要front加加即可，如果为空就不能删了。对于第二张图，当front指向数组的最后一个位置时，出队过后，front加加会越过数组，因此，每次出队列完成，都需要执行 front %= (k + 1) 这条语句，情况其实与上面入队列时的rear一样。

入队列与出队列介绍过了，后面就是一些队列基本的接口操作了。有取队头数据，取队尾数据，判空和判满，还有循环队列的销毁。

接下来就带大家来实现喽！

设计循环队列

  • 这里我们直接以题目的方式来实现，题目链接：-> 传送门 <-。

题目描述：设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

该题提供的需要我们实现的接口：

typedef struct {

} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) {

}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {

}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {

}

int myCircularQueueFront(MyCircularQueue* obj) {

}

int myCircularQueueRear(MyCircularQueue* obj) {

}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {

}

bool myCircularQueueIsFull(MyCircularQueue* obj) {

}

void myCircularQueueFree(MyCircularQueue* obj) {

}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35

接下来，就是对循环队列的一系列功能接口的实现了：

1.

  • 首先当然是定义一个循环队列的结构体。

相关代码实现：

// 循环队列的结构
typedef struct {
// 底层存储结构为数组
    int* a;
    // 指向队头
    int front;
    // 指向队尾
    int rear;
    // 规定的循环队列的长度
    // 这里存放一下规定的循环队列的长度是为了后面取模更方便
    int k;
} MyCircularQueue;

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12

2.

  • 然后便是对一个循环队列的创造。

  • 这里开辟一段连续的空间，可以存放规定的长度加一个数据，但其实总有一个空间是用不上的。

  • 然后将front与rear都指向循环队列的队头，就是置为0。

  • 最后将规定的长度存起来即可。

相关代码实现：

// 循环队列的创造（构造器），规定创造的循环队列的长度为k
MyCircularQueue* myCircularQueueCreate(int k) {
// 先开辟一个循环队列的空间
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    // assert防止开辟空间失败
    assert(obj);

// 多开一个空间，也就是开辟（k + 1）个数据空间
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    // 开始头指针和尾指针都指向0（也就是队头）
    obj->front = obj->rear = 0;
    // 存放规定的队列长度
    obj->k = k;

    return obj;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

3.

  • 这里是入队列的实现。
  • 入队列就是在当前的rear位置插入数据，然后rear加加。
  • 根据前面的解析，入队列之后都需要取模一次，避免rear越过数组。（当然也可以通过判断的方式来处理特殊情况）
  • 当队列为满的时候就不能入队列了。

相关代码实现：

// 入队列插入数据，插入成功返回true，不成功（队列已满）那就返回false
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
// 如果此时循环队列已经满了，说明入队列不能进行，直接返回 false
    if (myCircularQueueIsFull(obj)) return false;

// 在rear位置上插入数据，然后rear加加
    obj->a[obj->rear ++ ] = value;
    // 每次都模上个 （k + 1）
    obj->rear %= (obj->k + 1);

// 入队列成功返回true
    return true;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

4.

  • 接下来是出队列操作。
  • 出队列就是front加加，根据前面的讲解，每次出队列后都要记得需模上(k + 1)。（当然也可以通过判断的方式来处理特殊情况）
  • 当队列为空的时候就不能出队列了。

相关代码实现：

// 出队列删除数据，删除成功返回true，不成功（队列为空）那就返回false
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
// 当循环队列为空，说明不能再出队列了，表明出队列失败，直接返回false
    if (myCircularQueueIsEmpty(obj)) return false;

// 出队列直接front加加
    obj->front ++ ;
    // 每次都模上个 （k + 1）
    obj->front %= (obj->k + 1);

// 出队列成功返回true
    return true;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

5.

  • 获取队头数据，直接返回front此时指向的那个位置上的数据即可。
  • 如果循环队列为空的话，就取不了了，依题目要求直接返回-1。

相关代码实现：

// 获取队头元素，如果队列为空，返回-1
int myCircularQueueFront(MyCircularQueue* obj) {
// 如果循环队列为空，说明没有数据，直接返回-1
    if (myCircularQueueIsEmpty(obj)) return -1;
    return obj->a[obj->front];
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6

6.

  • 获取队尾数据，根据前面的分析，采用取模的方式获取。（当然也可以通过判断的方式）
  • 如果循环队列为空的话，就取不了了，依题目要求直接返回-1。

相关代码实现：

// 获取队尾元素，如果队列为空，返回-1
int myCircularQueueRear(MyCircularQueue* obj) {
// 如果循环队列此时为空，直接返回-1
    if (myCircularQueueIsEmpty(obj)) return -1;
    
    // 以取模的方式来获取
    return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

7.

  • 对于判空，就是判断front是否等于rear即可。

相关代码实现：

// 判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}

  • 1
  • 2
  • 3
  • 4

8.

  • 对于判满，根据前面的分析，也是通过取模的方式来实现的。（当然也可以通过判断的方式来处理特殊情况）

相关代码实现：

// 判满
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

  • 1
  • 2
  • 3
  • 4

9.

  • 最后就是销毁循环链表，malloc了几次，就free（释放）几次。

相关代码实现：

// 销毁循环队列
void myCircularQueueFree(MyCircularQueue* obj) {
// 有内到外依次释放空间
// 释放数组
    free(obj->a);
    // 释放循环队列
    free(obj);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

整体的代码

// 循环队列的结构
typedef struct {
// 底层存储结构为数组
    int* a;
    // 指向队头
    int front;
    // 指向队尾
    int rear;
    // 规定的循环队列的长度
    int k;
} MyCircularQueue;

// 在这声明一下判空和判满
bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);

// 循环队列的创造（构造器），规定创造的循环队列的长度为k
MyCircularQueue* myCircularQueueCreate(int k) {
// 先开辟一个循环队列的空间
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    // assert防止开辟空间失败
    assert(obj);

// 多开一个空间，也就是开辟（k + 1）个数据空间
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    // 开始头指针和尾指针都指向0（也就是队头）
    obj->front = obj->rear = 0;
    // 存放规定的队列长度
    obj->k = k;

    return obj;
}

// 入队列插入数据，插入成功返回true，不成功（队列已满）那就返回false
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (myCircularQueueIsFull(obj)) return false;

    obj->a[obj->rear ++ ] = value;
    obj->rear %= (obj->k + 1);

    return true;
}

// 出队列删除数据，删除成功返回true，不成功（队列为空）那就返回false
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj)) return false;

    obj->front ++ ;
    obj->front %= (obj->k + 1);

    return true;
}

// 获取队头元素，如果队列为空，返回-1
int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj)) return -1;
    return obj->a[obj->front];
}

// 获取队尾元素，如果队列为空，返回-1
int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj)) return -1;
    return obj->a[(obj->rear + obj->k) % (obj->k + 1)];
}

// 判空
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}

// 判满
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear + 1) % (obj->k + 1) == obj->front;
}

// 销毁循环队列
void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80

📯写在最后

💝设计一个循环队列还是有些复杂的呢，不过看过本文章，相信大家也可以轻松拿捏。
❤️‍🔥后续将会持续输出有关数据结构与算法的文章，你们的支持就是我写作的最大动力！

感谢阅读本小白的博客，错误的地方请严厉指出噢~

文章知识点与官方知识档案匹配，可进一步学习相关知识
算法技能树首页概览42126 人正在系统学习中
【算法系列篇】滑动窗口
走进人工智能|深度学习 算法的创世纪