🏆作者主页：king&南星
🎄专栏链接：数据结构

🌱树

一、🌲概念与定义

描述树结构：

1. 和现实世界的树 反着画
2. 根节点 枝干 叶子节点
3. 同一层 兄弟 上层：父 叔叔 上层的上层：爷爷
   下层：孩子 侄儿
4. 树的高度：几代人
5. 树退化成线性结构 ： 一叉树(链表) N代单传
   图解：
   现实中的树
   
   数据结构中的树是和现实倒着的
   
   
   详细解读：三个指针描述，一个指针指向父亲，一个指针指向兄弟，一个指针指向孩子，同时规则设定只有父亲的第一个孩子才可以有孩子

二、🌳定义与预备

先准备好头文件、结构体和函数声明

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef struct treeNode
{
int data;                  //数据
struct treeNode* pParent;  //指向父
struct treeNode* pBrother; //指向第一个兄弟
struct treeNode* pChild;   //指向第一个孩子
}treeNode;

#define SIZE sizeof(treeNode)

//创建节点函数
treeNode* createNode(int data);

//在树中找一个节点，找到返回这个节点的地址，找不到返回NULL
treeNode* findNode( treeNode* root, int findData);

//插入一个节点到树中
//把insertData插入到*pRoot树中 如果isChild为真成为findData节点的孩子，否则成为findData节点的兄弟
bool intsertNode( treeNode** pRoot, int findData, int insertData, bool isChild);

//遍历
void print_Tree(treeNode* root);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

三、🌴创建结点函数

这里利用一个技巧，直接使用内存设置函数memset函数，把三个指针内存都设置为0

treeNode* createNode( int data )
{
treeNode* newNode = (treeNode*)malloc(SIZE);
assert(newNode);
memset(newNode, 0, SIZE);//内存都设置为0
newNode->data = data;
return newNode;
}
1
2
3
4
5
6
7
8

四、🍀查找

在树中找一个节点，找到返回这个节点的地址，找不到返回NULL
先在while循环中遍历同一层的兄弟，直到他下一个兄弟为空，切换到下一层，如此循环下去，如果找到则返回地址，如果没找到则返回空

treeNode* findNode(treeNode* root, int findData) 
{
if (NULL == root) return NULL;  //防呆
treeNode* pTemp;
treeNode* pnextChild = root;
while (true)
{
pTemp = pnextChild;
if (NULL == pnextChild) break;
while( true )
{
//遍历兄弟层
if (NULL == pTemp) break;
if (findData == pTemp->data) return pTemp;
pTemp = pTemp->pBrother;
}
//切换到下一层(孩子)
pnextChild = pnextChild->pChild;
}
return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

五、🍁插入

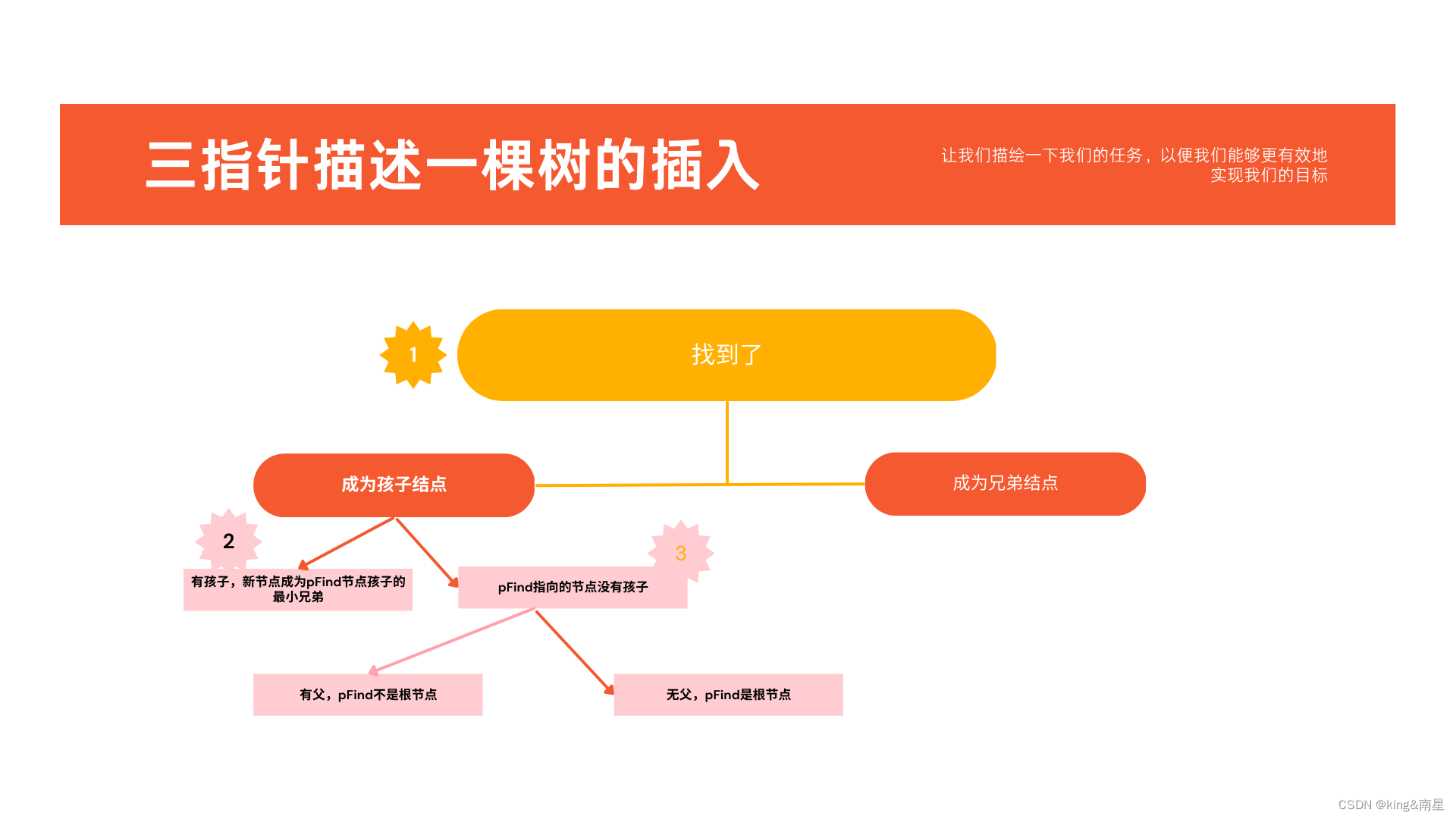
描述：插入一个节点到树中，把insertData插入到*pRoot树中 如果isChild为真成为findData节点的孩子，否则成为findData节点的兄弟

bool intsertNode(treeNode** pRoot, int findData, int insertData, bool isChild)
{
if (NULL == pRoot) return false; //防呆
if (NULL == *pRoot) //空树
{
*pRoot = createNode(insertData);
return true;
}
treeNode* pFind = findNode(*pRoot, findData);  //查找
if (NULL == pFind) return false;
treeNode* pNew, * pTemp;
//找到了
if (isChild) //新节点成为pFind指向节点的孩子
{
//有孩子，新节点成为pFind节点孩子的最小兄弟
if (pFind->pChild)
{
pTemp = pFind->pChild;
pNew = createNode(insertData);
while (pTemp->pBrother) pTemp = pTemp->pBrother;
pTemp->pBrother = pNew;
pNew->pParent = pFind;
return true;
}
//pFind指向的节点没有孩子
else
{
//有父，pFind不是根节点
if (pFind->pParent)
{
//pFind是pFind->pPartent的第一个孩子
if (pFind->pParent->pChild == pFind)
{
pNew = createNode(insertData);
pFind->pChild = pNew;
pNew->pParent = pFind;
return true;
}
else
{
//pFind不是pFind->pParent的第一个孩子
//新节点只能成为 pFind->pParent->pChild的孩子
intsertNode(&(pFind->pParent), pFind->pParent->pChild->data, insertData, true);
}
}
//无父，pFind是根节点
else
{
pNew = createNode(insertData);
pFind->pChild = pNew;
pNew->pParent = pFind;
return true;
}
}
}
else //新节点成为pFind指向节点的兄弟
{
pTemp = pFind;
while (pTemp->pBrother) pTemp = pTemp->pBrother;
pNew = createNode(insertData);
pTemp->pBrother = pNew;
pNew->pParent = pFind->pParent;
return true;
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

六、🍃遍历

和查找函数异曲同工

void print_Tree(treeNode* root) 
{
if (NULL == root) return NULL;  //防呆
treeNode* pTemp;
treeNode* pnextChild = root;
int cnt = 1;
while (true)
{
pTemp = pnextChild;
if (NULL == pnextChild) break;
printf("第[%d]层：", cnt++);
while (true)
{
//遍历兄弟层
if (NULL == pTemp) break;
printf("%d ", pTemp->data);
pTemp = pTemp->pBrother;
}
printf("\n");
//切换到下一层(孩子)
pnextChild = pnextChild->pChild;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

🎉欢迎各位→点赞👏 + 收藏💞 + 留言🔔​
💬总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流 🐾