方差分析的基本原理:
(1)将数据总的偏差平方和按照产生的原因分解成:
(总的偏差平方和)=(由因素水平引起的偏差平方和)+(试验误差平方和)
(2)上式右边两个平方和的相对大小可以说明因素的不同水平是否使得各型号的平均 维修时间产生显著性差异,为此需要进行适当的统计假设检验。
【例 1 】某公司采用四种方式推销其产品。为检验不同方式推销产品的效果,随机抽样得下表,不同的销售方式对销售量有影响吗?
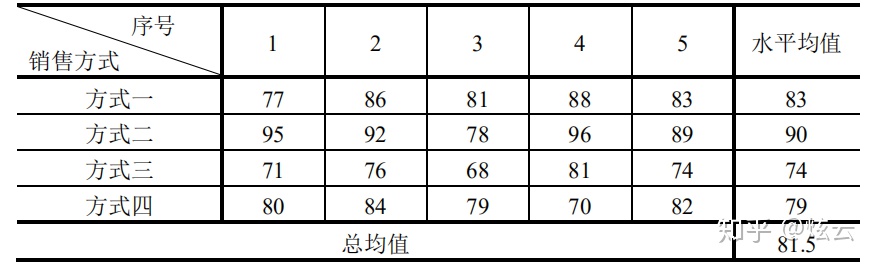
1. 因素(Factor)
因素是指所要研究的变量,它可能对因变量产生影响。在例 1 中,要分析不同销售方 式对销售量是否有影响,所以,销售量是因变量,而销售方式是可能影响销售量的因素。 如果方差分析只针对一个因素进行,称为单因素方差分析。如果同时针对多个因素进行, 称为多因素方差分析。本章介绍单因素方差分析和双因素方差分析,它们是方差分析中最常 用的。
在方差分析中, 通常把研究对象的特征值, 即所考察的试验结果称为试验指标. 本例中“销售量”就是试验指标.
2. 水平(Level)
水平指因素的具体表现,如销售的四种方式就是因素的不同取值等级。有时水平是人为划分的,比如质量被评定为好、中、差。
3. 单元(Cell)
单元指因素水平之间的组合。例 1 中销售方式一下的五种不同的销售业绩就构成一个单元。方差分析要求的方差齐性就是指的各个单元间的方差齐性。
4. 元素(Element)
元素指用于测量因变量的最小单位。一个单元里可以只有一个元素,也可以有多个元素。 例 1 中各单元中有 5 个元素。
5. 均衡(Balance)
如果一个试验设计中任一因素各水平在所有单元格中出现的次数相同,且每个单元格内 的元素数相同,则称该试验是为均衡,否则,就被称为不均衡。不均衡试验中获得的数据在 分析时较为复杂。例 1 是均衡的。
6. 交互作用(Interaction)
如果一个因素的效应大小在另一个因素不同水平下明显不同,则称为两因素间存在交互 作用。当存在交互作用时,单纯研究某个因素的作用是没有意义的,必须在另一个因素的不 同水平下研究该因素的作用大小。如果所有单元格内都至多只有一个元素,则交互作用无法 测出。
要看不同推销方式的效果,其实就归结为一个检验问题,设
从表 1 可以看到,20 个数据各不相同,这种差异可能由两方面的原因引起的:一是推销方式的影响,不同的方式会使人们产生不同消费冲动和购买欲望,从而产生不同的购买行 动,这种由不同水平造成的差异,我们称为系统性差异;另一是随机因素的影响,同一种推 销方式在不同的工作日销量也会不同,因为来商店的人群数量不一,经济收入不一,当班服 务员态度不一,这种由随机因素造成的差异,我们称为随机性差异。
两个方面产生的差异用 两个方差来计量:一是组内方差,即水平内部的方差,仅包含随机性差异;一是组间方差, 即
如果不 同的水平对结果没有影响,如推销方式对销售量不产生影响,那么在组间方差中,也就仅仅包含随机性差异,而没有系统性差异,它与组内方差就应该很接近,两个方差的比值就会约 等于 1;反之,如果不同的水平对结果产生影响,在组间方差中系统性差异就会很明显,此 时组间方差就会大于组内方差,两个方差的比值就会远大于 1,当这个比值大到某个程度时, 即达到某临界点,我们就做出判断,不同的水平之间存在着显著性差异。因此,方差分析就 是通过对组间方差和组内方差的比较,做出原假设拒绝与否的判断。
进行方差分析,样本通常要符合以下假定:首先是各样本的独立性,即各组观察数据, 是从相互独立的总体中抽取的,只有是独立的随机样本,才能保证方差的可加性;其次要求 所有观察值都是从正态总体中抽取,且方差相等。
在实际应用中样本能够严格满足这些假定条件的很少,在社会经济现象中更是如此。但 一般应近似地符合上述要求,背离假定太多,就不宜用方差分析了。
【单因素方差分析实例】四个实验小组,分别用不同的记忆方法记忆英语单词,经过一段时 间后,统一测验记忆情况,结果如下,问四种记忆方法有无显著性差异?
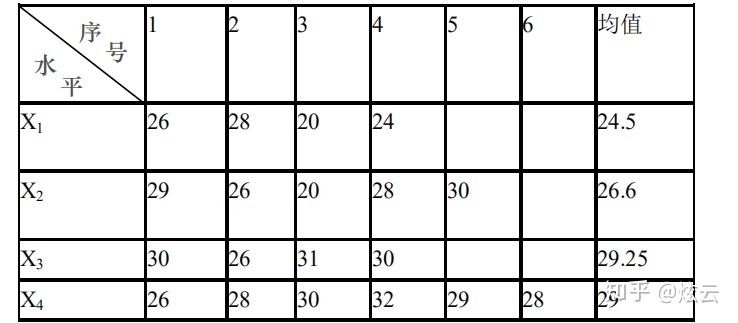
【双因素方差分析实例】在实际问题的研究中,有时需要考虑两个因素对实验结果的影响。
例如饮料销售,除了关心饮料颜色之外,我们还想了解销售地区是否影响销售量,如果 在不同的地区,销售量存在显著的差异,就需要分析原因。采用不同的销售策略,使该饮料 品牌在市场占有率高的地区继续深入人心,保持领先地位;在市场占有率低的地区,进一步 扩大宣传,让更多的消费者了解、接受该生产线。 若把饮料的颜色看作影响销售量的因素 A,饮料的销售地区则是影响因素 B。对因素 A 和因素 B 同时进行分析,就属于双因素方差分析。
双因素方差分析的内容,是对影响因素进行检验,究竟是一个因素在起作用,还是两个 因素都起作用,或是两个因素的影响都不显著。