回顾上一篇单因素方差分析的一个例子：

matlab代码：

clc, clear,close all
a=readmatrix('data14_2.txt')
[p.tst]=anova1(a)

因为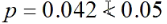，所以这几种工艺制成的灯泡寿命有显著差异。

箱线图如图所示： 

双因素方差分析

单因素方差分析仅考虑了一个分类型自变量对数值型因变量的影响。但在实际应用中，考虑多个因素对试验结果影响的情况也是存在的。例如在分析影响某种产品销量的因素时，就通常需要考虑品牌、价格和区域等多个因素的影响。特别地，如果方差分析中涉及两个分类型自变量时，就通常将其称为双因素方差分析。

记两个因素分别为A,B，设A取s个水平，B取r个水平，并且服从正态分布。如下图排列。


1.无交互作用
在双因素方差分析中,被纳入考虑范畴的两个影响因素对于因变量的作用是彼此独立的，这时的双因素方差分析称为无交互作用的双因素方差分析，或称为无重复双因素分析。在每个水平(B,A,)下只要做一次试验，即错误!未找到引用源。

双因素方差分析与单因素方差分析的基本原理相同,仍然是从反映全部试验数据间大小不等状况的总变异开始。总变异用总离差平方和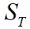,表示，它是全部样本观测值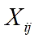。与总的样本平均值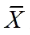差的平方和。

检验规则为：

 例子：

 方差分析表如图所示：由p值可知化肥和小麦种子对小麦产量无显著影响。

 matlab代码：

clc， clear,close all
a=readmatrix (' data14_3.txt’)
[p.t.st]=anova2(a)

 2.有交互作用

与无交互作用的双因素方差分析相比，有交互作用的情况则会显得更加复杂。此时，被纳入考虑的两个影响因素除了对因变量独自发挥作用以外,它们的搭配也会对因变量产生一种新的影响。

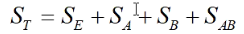
 如下图形式的为双因素方差分析表：

 例题：

 matlab代码：

clc，clear，close all
a=readmatrix (’ data14_4.txt')
[p,t,st]=anova2(a,3)

3.方差齐性的检验方法
方差分析的一个前提条件是相互比较的各样本的总体方差相等，即具有方差齐性，这就需要在作方差分析之前，先对数据的方差齐性进行检验，特别是在样本方差相差悬殊时，应注意这个问题。本节介绍两种多样本方差齐性的检验方法，即 Bartlett检验法和Levene检验法。