一、概念

二叉搜索树任意节点有以下的性质：

• 若左子树不为空，则左子树的所有节点的值小于根节点
• 若右子树不为空，则右子树的所有节点的值大于根节点
• 它的左右子树也同样是二叉搜索树

根据以上的性质，我们发现二叉搜索树如果使用中序遍历，那么结果就是有序的。

二、基本操作

树的结构：

template <class K>
struct BSTreeNode
{
BSTreeNode(K x)
: _left(nullptr)
, _right(nullptr)
, _key(x)
{}
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
};
1
2
3
4
5
6
7
8
9
10
11
12

2.1 查找

根据搜索二叉树的性质
当要查找的值比当前节点小，则继续在当前节点的左子树找。
当要查找的值比当前节点大，则继续在当前节点的右子树找。
相等的时候就返回true即可。
如果找到空都没找到即不存在，返回false。

bool Find(const K& x)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > x)
{
cur = cur->_left;
}
else if (cur->_key < x)
{
cur = cur->_right;
}
else return true;
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2.2 插入

插入的时候要注意根节点为空的情况，此时新增节点直接给_root即可。
当根节点不为空的时候，我们可以定义一个cur，根据查找的方法查找到为空为止，在此处新增节点，为了让新增节点链接上，我们需要添加一个parent指针记录父节点。
注意不能插入相同的节点，当发现相同时，就返回false。

bool Insert(const K& x)
{
if (_root == nullptr)
{
_root = new Node(x);
return true;
}
else
{
Node* cur = _root, *parent = nullptr;
while (cur)
{
if (cur->_key < x)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > x)
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(x);
if (parent->_key > x) parent->_left = cur;
else parent->_right = cur;
return true;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.3 删除

1️⃣ 左为空或者右为空（包含左右都为空），删除自己后要把自己的父亲和孩子节点链接起来。
这里要注意删除根节点的情况，要替换_root的位置。

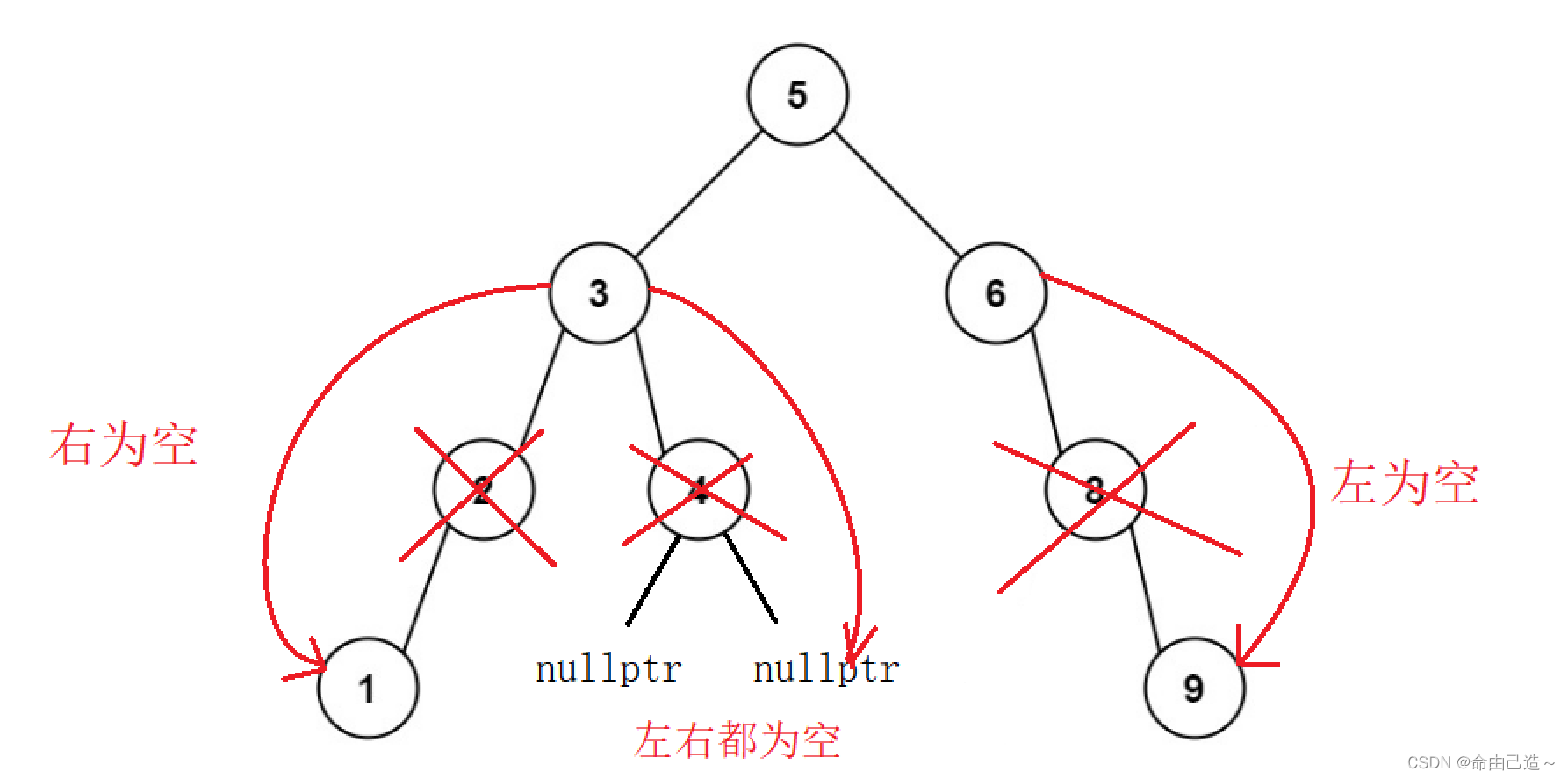
2️⃣ 左右都不为空，我们需要把当前节点右子树的最小节点或者左子树的最大节点进行替换，然后删除替换节点即可。
我们就用右子树的最大值进行替换。

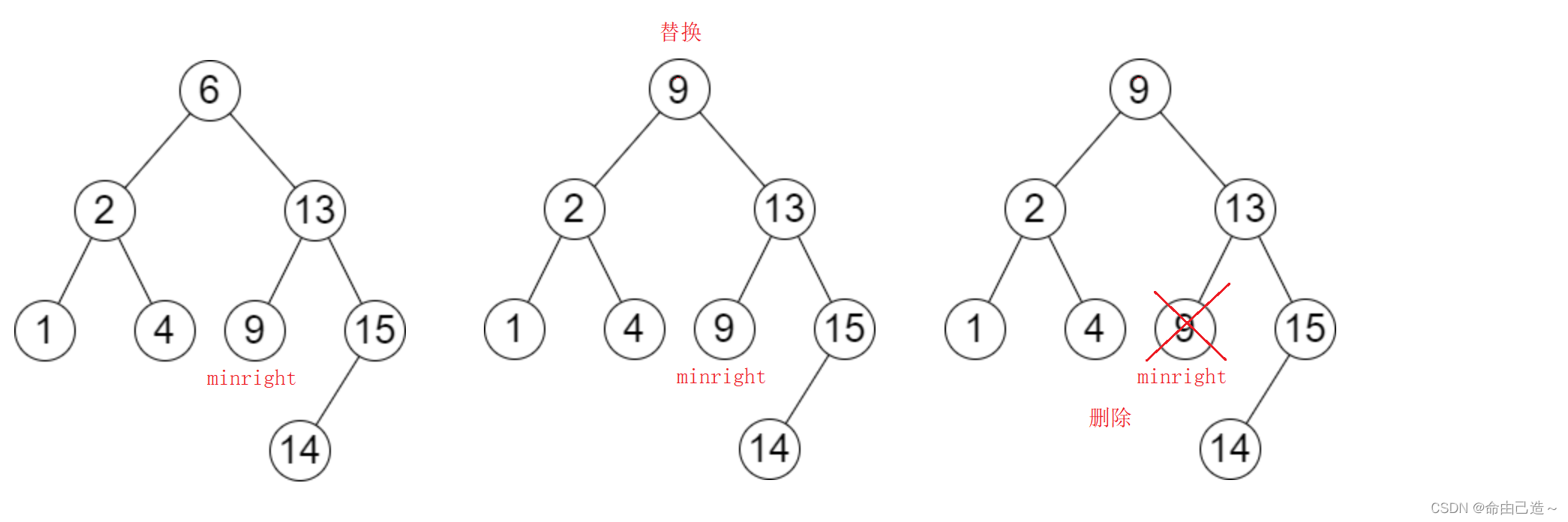
bool Erase(const K& x)
{
Node* cur = _root, *parent = nullptr;
while (cur)
{
if (cur->_key < x)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > x)
{
parent = cur;
cur = cur->_left;
}
else// 删除
{
if (cur->_left == nullptr)
{
if (parent == nullptr)
{
_root = cur->_right;
delete cur;
return true;
}
//判断cur是parent的谁
if (cur == parent->_left)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
delete cur;
return true;
}
else if(cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
delete cur;
return true;
}
//判断cur是parent的谁
if (cur == parent->_left)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
delete cur;
return true;
}
else// 左右都不为空
{
// 找右子树的最左节点
Node* minRight = cur->_right;
Node* parent = cur;
while (minRight->_left)
{
parent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (minRight == parent->_left)
{
parent->_left = nullptr;
}
else parent->_right = nullptr;
delete minRight;
return true;
}
}
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

2.4 中序遍历

void InOrder(Node* root)
{
if (!root) return;
InOrder(root->_left);
cout << root->_key << " ";
InOrder(root->_right);
}

void InOrder()
{
InOrder(_root);
}
1
2
3
4
5
6
7
8
9
10
11
12

三、递归写法

3.1 查找

bool FindR(Node* root, const K& x)
{
if (root == nullptr) return false;
if (x < root->_key) return FindR(root->_left, x);
else if (x > root->_key) return FindR(root->_right, x);
else return true;
}

bool FindR(const K& x)
{
return FindR(_root, x);
}
1
2
3
4
5
6
7
8
9
10
11
12

3.2 插入

插入的时候我们不方便找到父节点，所以我们可以使用
Node*& root，这样这个节点就是上一个节点左或右节点的指针的引用，所以改变root就可以改变父亲。

bool InsertR(Node*& root, const K& x)
{
if (root == nullptr)
{
root = new Node(x);
return true;
}
if (x < root->_key) return InsertR(root->_left, x);
else if (x > root->_key) return InsertR(root->_right, x);
else return false;
}

bool InsertR(const K& x)
{
return InsertR(_root, x);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3.3 删除

当左右子树都不为空的时候我们把右子树的最小节点赋值给当前节点后，再递归删除右子树的最小节点。

bool EraseR(Node*& root, const K& x)
{
if (root == nullptr) return false;
if (x < root->_key) return EraseR(root->_left, x);
else if (x > root->_key) return EraseR(root->_right, x);
else
{
if (root->_left == nullptr)
{
Node* del = root;
root = root->_right;
delete del;
return true;
}
else if (root->_right == nullptr)
{
Node* del = root;
root = root->_left;
delete del;
return true;
}
else
{
Node* minRight = root->_right;
while (minRight->_left)
{
minRight = minRight->_left;
}
root->_key = minRight->_key;
return EraseR(root->_right, minRight->_key);
}
}
}

bool EraseR(const K& x)
{
return EraseR(_root, x);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

四、k与kv模型

1️⃣ k模型
结构中只存储key即可，它的作用是判断关键字是否存在。
2️⃣ kv模型
每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。可以通过key查找或修改Value。

template <class K, class V>
struct BSTreeNode
{
BSTreeNode(K x, V y)
: _left(nullptr)
, _right(nullptr)
, _key(x)
, _val(y)
{}
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _val;
};

template <class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
bool Insert(const K& x, const V& y)
{
if (_root == nullptr)
{
_root = new Node(x, y);
return true;
}
else
{
Node* cur = _root, *parent = nullptr;
while (cur)
{
if (cur->_key < x)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > x)
{
parent = cur;
cur = cur->_left;
}
else return false;
}
cur = new Node(x, y);
if (parent->_key > x) parent->_left = cur;
else parent->_right = cur;
return true;
}
}

Node* Find(const K& x)
{
Node* cur = _root;
while (cur)
{
if (cur->_key > x)
{
cur = cur->_left;
}
else if (cur->_key < x)
{
cur = cur->_right;
}
else return cur;
}
return nullptr;
}

void InOrder(Node* root)
{
if (!root) return;
InOrder(root->_left);
cout << root->_key << " ";
InOrder(root->_right);
}

void InOrder()
{
InOrder(_root);
}

private:

void Destory(Node*& root)
{
if (root == nullptr) return;
Destory(root->_left);
Destory(root->_right);
delete root;
}

Node* _root = nullptr;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94