一、unordered系列关联式容器

map和set的底层是用红黑树实现的，在最差的情况下也能在高度次查询到节点。但是当节点数量非常多的时候，效率并不理想，所以C++11引入了unorderedmap与unorderedset，能极快的查找到元素节点，但是它们的底层不是用搜索树实现的，所以不能保证有序。

二、哈希原理

2.1 哈希映射

红黑树我们需要进行比较查找才能找到对应节点。而进过哈希映射函数，让key值跟存储位置建立映射关系，那么在查找时通过该函数可以很快找到该元素。
像计数排序就可以看作一个简单的哈希映射，叫做直接定址法，但是得范围集中才行。
如果范围不集中，就可以用除留余数法，我们可以用元素的值去模上容器的大小。这样所有的元素就一定能存入表中。

2.2 哈希冲突

上面的除留余数法可能会导致两个元素要存储在同一个位置。我们把这种情况称为哈希冲突。而解决哈希冲突的方法有两种

2.2.1 闭散列—开放地址法

闭散列的大致方法就是：当映射的地方已经有值了，那么就按规律找其他位置。而查找空位的方法又分为线性探测和二次探测。

【线性探测】
插入：
用除留余数法求出key值的关键码，并将它放到对应的位置上。如果该位置已经存在数据被占用了，那么继续寻找下一个位置，也就是+1的位置，如果+1的位置已经有数据，那么继续+1，直到寻找到下一个空位置为止。

查找：
查找就是取余后往后探索，知道找到空位置就停止，这里要注意如果删除了一个数据，而要查找的元素在删除位置的后边，就会在删除的地方停下来，导致本来存在的元素查找不到。
解决这种情况的方式：
可以再设置一种状态（枚举），将数组中每个数据的状态记录一下，所以就有了存在，空和删除这三种状态。删除的位置状态时删除，查找的时候不会停下。
这里要注意有一种情况是整个闭散列全部都存在或者为删除状态（边插入边删除不会扩容），所以最多循环一圈。

负载因子：
表中的有效数据个数/表的大小，载荷因子不能超过1。为了减小冲突，一般到0.7就会扩容。

字符串哈希：
这里要注意如果key是字符串就不能使用除法取余，所以我们需要一个仿函数把字符串转换成数字。

【二次探测】
我们知道线性探测如果发生了冲突并且冲突连在一起就会引起数据堆积，导致搜索效率降低，为了解决这种情况，就有了二次探测。
二次探测的方法就是以i的2次方去进行探测，如果要找的位置Idx被占，下次找Idx + 1^2，如果再次被占，则找Idx + 2^2，以此类推。

2.2.2 代码实现

// 状态
enum Sta
{
EXIST,
DELETE,
EMPTY,
};

// 数据类型
template <class K, class V>
struct HashData
{
pair<K, V> _kv;
Sta _state = EMPTY;
};

template <class K>
struct HashKey
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};

// 字符串哈希
template <>
struct HashKey<string>
{
size_t operator()(const string& key)
{
size_t ans = 0;
for (int i = 0; i < key.size(); i++)
{
ans *= 131;
ans += key[i];
}
return ans;
}
};

// 哈希表结构
template <class K, class V, class GetKey = HashKey<K>>
class HashTable
{
typedef HashData<K, V> data;
public:
HashTable()
: _n(0)
{
_tables.resize(7);
}

bool insert(const pair<K, V>& kv)
{
// 重复
if (find(kv.first)) return false;
// 负载因子
size_t load = _n * 10 / _tables.size();
if (load >= 10)
{
// 出作用域后销毁
HashTable<K, V> newhash;
newhash._tables.resize(2 * _tables.size());
for (auto& e : _tables)
{
if (e._state == EXIST)
{
newhash.insert(e._kv);
}
}
_tables.swap(newhash._tables);
}
GetKey Get;
size_t hashI = Get(kv.first) % _tables.size();
while (_tables[hashI]._state == EXIST)
{
++hashI;
hashI %= _tables.size();
}
_tables[hashI]._kv = kv;
_tables[hashI]._state = EXIST;
++_n;
return true;
}

data* find(const K& key)
{
GetKey Get;
size_t hashI = Get(key) % _tables.size();
size_t startI = hashI;// 最多循环一圈
while (_tables[hashI]._state != EMPTY)
{
if (_tables[hashI]._state == EXIST
&& _tables[hashI]._kv.first == key)
{
return &_tables[hashI];
}
++hashI;
hashI %= _tables.size();
if (hashI == startI) break;
}
return nullptr;
}

bool erase(const K& key)
{
data* node = find(key);
if (node)
{
node->_state = DELETE;
return true;
}
return false;
}
private:
vector<data> _tables;
size_t _n;// 有效数据个数
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119

2.2.3 开散列—拉链法

闭散列解决哈希冲突的办法就是抢占别人的位置，而开散列不一样，冲突的元素可以一起在同一个位置。
首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

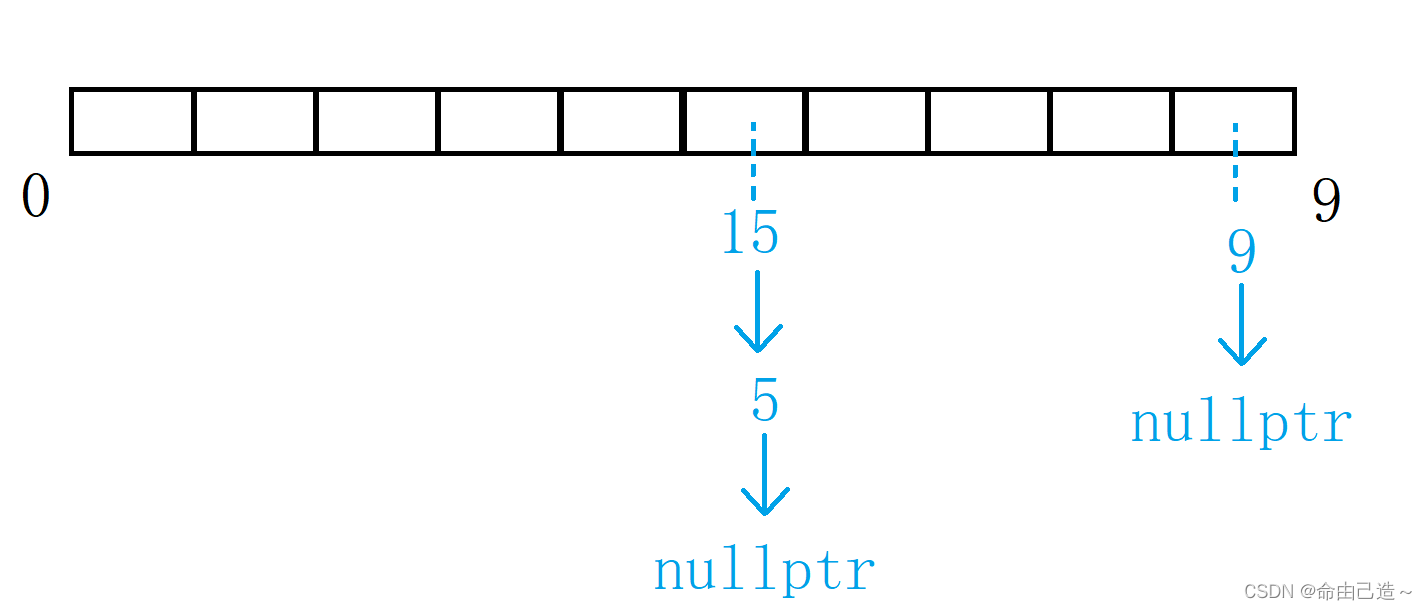
【增容】
随着插入的数量增加，可能导致一个桶的节点数目非常多，为了应对这种情况，在一定情况下需要增容。一般当负载因子为1的时候扩容。

2.2.4 代码实现

template <class K, class V>
struct HashNode
{
HashNode(const pair<K, V> kv)
: _kv(kv)
, _next(nullptr)
{}

pair<K, V> _kv;
HashNode<K, V>* _next;
};

template <class K, class V, class GetKey = HashKey<K>>
class HashTable
{
typedef HashNode<K, V> Node;
public:
HashTable()
: _n(0)
{
_tables.resize(10);
}

~HashTable()
{
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}

bool insert(const pair<K, V>& kv)
{
// 重复
if (find(kv.first))
return false;
// 负载因子为1扩容
if (_tables.size() == _n)
{
vector<Node*> newtable;
newtable.resize(2 * _n);
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t idx = GetKey()(cur->_kv.first) % newtable.size();
cur->_next = newtable[idx];
newtable[idx] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newtable);
}

GetKey Get;
size_t hashI = GetKey()(kv.first) % _tables.size();
Node* newnode = new Node(kv);
newnode->_next = _tables[hashI];
_tables[hashI] = newnode;
++_n;
return true;
}

Node* find(const K& key)
{
size_t idx = GetKey()(key) % _tables.size();
Node* cur = _tables[idx];
while (cur)
{
if (cur->_kv.first == key)
return cur;
else
cur = cur->_next;
}
return nullptr;
}

bool erase(const K& key)
{
size_t idx = GetKey()(key) % _tables.size();
Node* cur = _tables[idx];
Node* pre = nullptr;
while (cur)
{
if (cur->_kv.first == key)
{
if (pre = nullptr)
{
_tables[i] = nullptr;
}
else
{
pre->_next = cur->_next;
}
delete cur;
--_n;
return true;
}
else
{
pre = cur;
cur = cur->_next;
}
}
return false;
}
private:
vector<Node*> _tables;
size_t _n = 0;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120

三、哈希封装unordered_map/unordered_set

3.1 基本框架

这里的封装跟红黑树的类似，我们需要改变一下节点的结构，不管传入的是key还是pair，都用模板参数T接收。

template <class T>
struct HashNode
{
HashNode(const T& data)
: _data(data)
, _next(nullptr)
{}

T _data;
HashNode<T>* _next;
};
1
2
3
4
5
6
7
8
9
10
11

根据前面红黑树的封装可以知道传入的时候第一个参数主要用来查找和删除，第二个参数决定节点是什么类型。
代码如下：

// unordered_Set.h
template <class K, class Hash = HashKey<K>>
class unordered_set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
bool insert(const K& key)
{
return _ht.insert(key);
}
private:
hashbucket::HashTable<K, K, Hash, SetKeyOfT> _ht;
};

// unordered_Map.h
template <class K, class V, class Hash = HashKey<K>>
class unordered_map
{
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
bool insert(const T& data)
{
return _ht.insert(data);
}
private:
hashbucket::HashTable<K, pair<K, V>, Hash, MapKeyOfT> _ht;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

3.2 迭代器实现

3.2.3 operator*和operator->和operator!=

解引用operator*是将一个指针指向的内容取出来，它返回的是哈希节点的数据。operator->是将指针指向内容的地址取出来，也就是节点指向数据的地址。

T& operator*()
{
return _node->_data;
}

T* operator->()
{
return &_node->_data;
}

bool operator!=(const self& it) const
{
return _node != it._node;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

3.2.4 operator++与构造函数

如果这个桶没有走完，那么直接遍历当前迭代器指向节点的下一个节点。如果这个桶走完了，要遍历下一个桶。但是既然要遍历，那么一定需要_tables的大小，而_tables又是一个私有成员，随意我们可以用友元类来访问。

template<class K, class T, class GetKey, class KeyOfT>
friend struct HashIterator;// 迭代器需要访问私有
1
2

而且我们还需要_tables，所以在构造迭代器的时候要传进来个_tables的指针。

HashIterator(HT* ht, Node* node)// 传递指针
: _node(node)
, _ht(ht)
{}
1
2
3
4

operator++代码如下：

self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
// 找下一个桶
KeyOfT kot;
Hash hash;
size_t idx = hash(kot(_node->_data)) % _ht->_tables.size();
idx++;
while (idx < _ht->_tables.size())
{
if (_ht->_tables[idx] != nullptr)
{
_node = _ht->_tables[idx];
break;
}
else
{
idx++;
}
}

if (idx == _ht->_tables.size())
{
_node = nullptr;
}
}
return *this;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

3.2.5 begin()和end()

begin就是找到_tables表的第一个不为空的桶的头节点，如果找到了，返回第一个位置的迭代器，因为迭代器的构造需要节点指针和哈希表的指针，那么哈希表的指针是什么呢？哈希表的指针就是this，this代表了整个哈希表的指针。将this指针传给迭代器的构造，那么我们就能取到_table。
而end就是最后一个节点的下一个地址，也就是nullptr。

template <class K, class T, class GetKey, class KeyOfT>
class HashTable
{
typedef HashNode<T> Node;

template<class K, class T, class GetKey, class KeyOfT>
friend struct HashIterator;// 迭代器需要访问私有
public:
typedef HashIterator<K, T, GetKey, KeyOfT> iterator;
iterator begin()
{
for (size_t i = 0; i < _tables.size(); i++)
{
if (_tables[i])
{
return iterator(this, _tables[i]);
}
}
return iterator(this, nullptr);
}

iterator end()
{
return iterator(this, nullptr);
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

3.2.6 operator[]

[]在前面的红黑树的封装也出现过，operator[]只有map中有，因为operator[]可以对插入的值进行增加，查找。如果该值第一次出现，那么operator[]充当的是插入，如果该值第二次出现，那么operator[]就充当的是修改。
既然是对是否成功插入做判断，那么insert和find都要做出修改。

// unordered_Map.h
V& operator[](const K& key)
{
pair<iterator, bool> ret = _ht.insert(make_pair(key, V()));
return ret.first->second;
}

// HashTable.h
pair<iterator, bool> insert(const T& data)
{
// 重复
iterator it = find(KeyOfT()(data));
if (it != end())
{
return make_pair(it, false);
}
// 负载因子为1扩容
if (_tables.size() == _n)
{
vector<Node*> newtable;
newtable.resize(2 * _n);
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t idx = GetKey()(KeyOfT()(data)) % newtable.size();
cur->_next = newtable[idx];
newtable[idx] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newtable);
}

size_t hashI = GetKey()(KeyOfT()(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[hashI];
_tables[hashI] = newnode;
++_n;
return make_pair(iterator(this, newnode), true);
}

iterator find(const K& key)
{
size_t idx = GetKey()(key) % _tables.size();
Node* cur = _tables[idx];
while (cur)
{
if (KeyOfT()(cur->_data) == key)
return iterator(this, cur);
else
cur = cur->_next;
}
return end();
}

bool erase(const K& key)
{
size_t idx = GetKey()(KeyOfT()(key)) % _tables.size();
Node* cur = _tables[idx];
Node* pre = nullptr;
while (cur)
{
if (cur->_data == key)
{
if (pre = nullptr)
{
_tables[idx] = nullptr;
}
else
{
pre->_next = cur->_next;
}
delete cur;
--_n;
return true;
}
else
{
pre = cur;
cur = cur->_next;
}
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

3.2.7 const迭代器问题

在stl源码中可以看到并没有用以前的方法使用：

typedef _list_iterator<T, T&, T*> iterator;
typedef _list_iterator<T, const T&, const T*> const_iterator;
1
2

原因是如果使用const版本传递，那么_tables使用[]返回的就是const。而用const迭代器去构造 HT* _ht; Node* _node;就会导致权限放大，无法构造。但是如果改成 const HT* _ht; const Node* _node;，又会导致[]不能修改的问题。

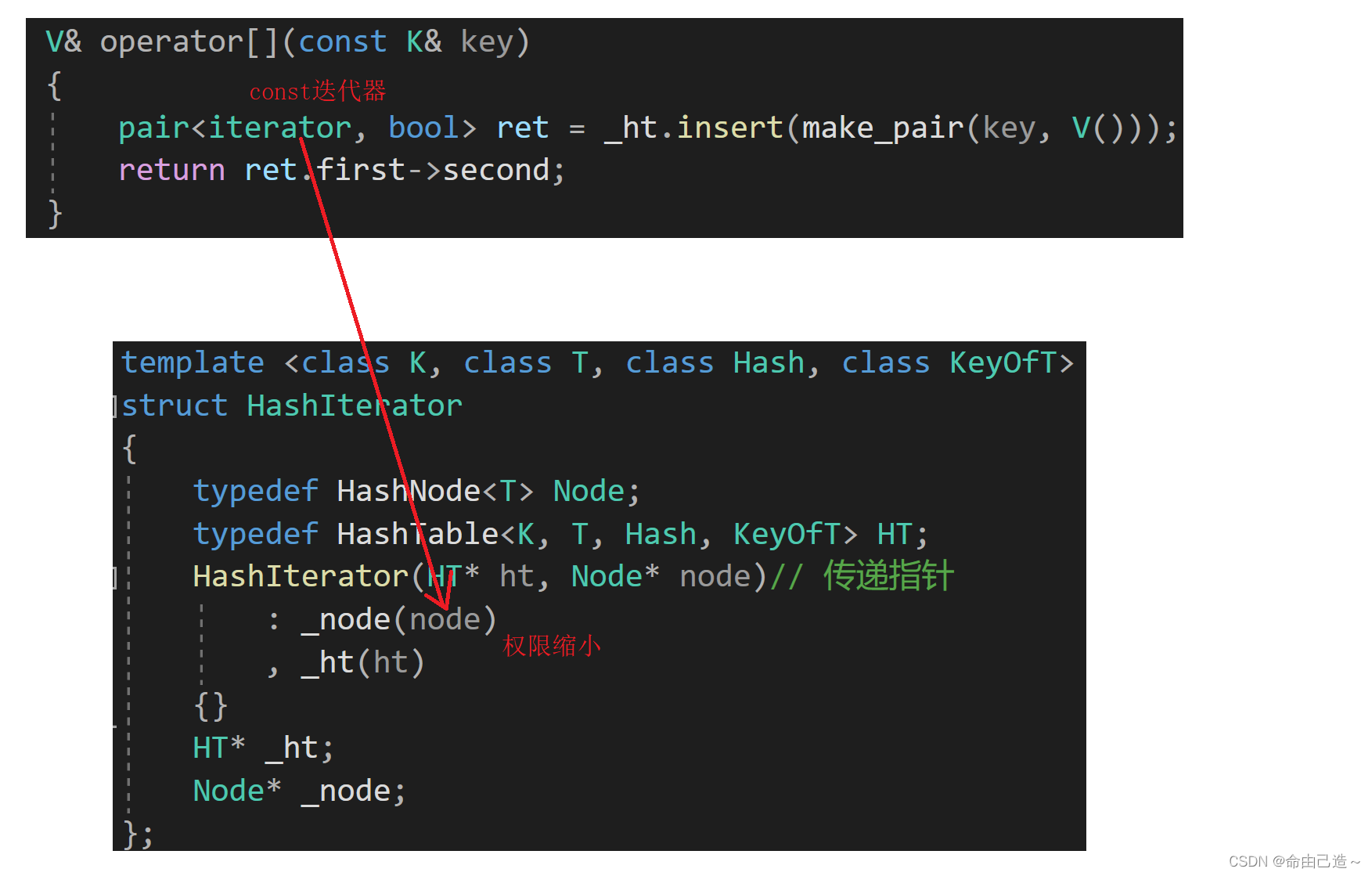
所以我们需要再写一个const版本迭代器：

template <class K, class T, class Hash, class KeyOfT>
struct ConstHashIterator
{
typedef HashNode<T> Node;
typedef ConstHashIterator<K, T, Hash, KeyOfT> self;
typedef HashTable<K, T, Hash, KeyOfT> HT;

ConstHashIterator(const HT* ht, const Node* node)// 传递指针
: _node(node)
, _ht(ht)
{}

const T& operator*() const
{
return _node->_data;
}

const T* operator->() const
{
return &_node->_data;
}

bool operator!=(const self& it) const
{
return _node != it._node;
}

self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
// 找下一个桶
KeyOfT kot;
Hash hash;
size_t idx = hash(kot(_node->_data)) % _ht->_tables.size();
idx++;
while (idx < _ht->_tables.size())
{
if (_ht->_tables[idx] != nullptr)
{
_node = _ht->_tables[idx];
break;
}
else
{
idx++;
}
}

if (idx == _ht->_tables.size())
{
_node = nullptr;
}
}
return *this;
}
const HT* _ht;
const Node* _node;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

往HashTable写入友元类：

template <class K, class T, class Hash, class KeyOfT>
friend struct ConstHashIterator;
1
2

添加cbegin()与cend()。

// unordered_Set.h
typedef typename hashbucket::HashTable<K, K, Hash, SetKeyOfT>::const_iterator const_iterator;

const_iterator cbegin()
{
return _ht.cbegin();
}

const_iterator cend()
{
return _ht.cend();
}

//unordered_Map.h
typedef typename hashbucket::HashTable<K, pair<K, V>, Hash, MapKeyOfT>::const_iterator const_iterator;

const_iterator cbegin()
{
return _ht.cbegin();
}

const_iterator cend()
{
return _ht.cend();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

四、哈希源码

unordered_set.h:

#pragma once
#include "HashTable.h"

namespace yyh
{
template <class K, class Hash = HashKey<K>>
class unordered_set
{
struct SetKeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
typedef typename hashbucket::HashTable<K, K, Hash, SetKeyOfT>::iterator iterator;
typedef typename hashbucket::HashTable<K, K, Hash, SetKeyOfT>::const_iterator const_iterator;
iterator begin()
{
return _ht.begin();
}

iterator end()
{
return _ht.end();
}

const_iterator cbegin()
{
return _ht.cbegin();
}

const_iterator cend()
{
return _ht.cend();
}

pair<iterator, bool> insert(const K& key)
{
return _ht.insert(key);
}

bool find(const K& key)
{
return _ht.find(key);
}

bool erase(const K& key)
{
return _ht.erase(key);
}

private:
hashbucket::HashTable<K, K, Hash, SetKeyOfT> _ht;
};
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

unordered_map.h:

#pragma once
#include "HashTable.h"

namespace yyh
{
template <class K, class V, class Hash = HashKey<K>>
class unordered_map
{
struct MapKeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename hashbucket::HashTable<K, pair<K, V>, Hash, MapKeyOfT>::iterator iterator;
typedef typename hashbucket::HashTable<K, pair<K, V>, Hash, MapKeyOfT>::const_iterator const_iterator;
iterator begin()
{
return _ht.begin();
}

iterator end()
{
return _ht.end();
}

const_iterator cbegin()
{
return _ht.cbegin();
}

const_iterator cend()
{
return _ht.cend();
}

pair<iterator, bool> insert(const pair<K, V>& kv)
{
return _ht.insert(kv);
}

bool find(const K& key)
{
return _ht.find(key);
}

bool erase(const K& key)
{
return _ht.erase(key);
}

V& operator[](const K& key)
{
pair<iterator, bool> ret = _ht.insert(make_pair(key, V()));
return ret.first->second;
}
private:
hashbucket::HashTable<K, pair<K, V>, Hash, MapKeyOfT> _ht;
};
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

HashTable.h：

#pragma once

#include <iostream>
#include <vector>
#include <string>
using namespace std;

template <class K>
struct HashKey
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};

// 字符串哈希
template <>
struct HashKey<string>
{
size_t operator()(const string& key)
{
size_t ans = 0;
for (size_t i = 0; i < key.size(); i++)
{
ans *= 131;
ans += s[i];
}
return ans;
}
};

namespace hashbucket
{
template <class T>
struct HashNode
{
HashNode(const T& data)
: _data(data)
, _next(nullptr)
{}

T _data;
HashNode<T>* _next;
};

// 前置声明
template <class K, class T, class Hash, class KeyOfT>
class HashTable;

template <class K, class T, class Hash, class KeyOfT>
struct HashIterator
{
typedef HashNode<T> Node;
typedef HashIterator<K, T, Hash, KeyOfT> self;
typedef HashTable<K, T, Hash, KeyOfT> HT;

HashIterator(HT* ht, Node* node)// 传递指针
: _node(node)
, _ht(ht)
{}

T& operator*()
{
return _node->_data;
}

T* operator->()
{
return &_node->_data;
}

bool operator!=(const self& it) const
{
return _node != it._node;
}

self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
// 找下一个桶
KeyOfT kot;
Hash hash;
size_t idx = hash(kot(_node->_data)) % _ht->_tables.size();
idx++;
while (idx < _ht->_tables.size())
{
if (_ht->_tables[idx] != nullptr)
{
_node = _ht->_tables[idx];
break;
}
else
{
idx++;
}
}

if (idx == _ht->_tables.size())
{
_node = nullptr;
}
}
return *this;
}

HT* _ht;
Node* _node;
};

template <class K, class T, class Hash, class KeyOfT>
struct ConstHashIterator
{
typedef HashNode<T> Node;
typedef ConstHashIterator<K, T, Hash, KeyOfT> self;
typedef HashTable<K, T, Hash, KeyOfT> HT;

ConstHashIterator(const HT* ht, const Node* node)// 传递指针
: _node(node)
, _ht(ht)
{}

const T& operator*() const
{
return _node->_data;
}

const T* operator->() const
{
return &_node->_data;
}

bool operator!=(const self& it) const
{
return _node != it._node;
}

self& operator++()
{
if (_node->_next)
{
_node = _node->_next;
}
else
{
// 找下一个桶
KeyOfT kot;
Hash hash;
size_t idx = hash(kot(_node->_data)) % _ht->_tables.size();
idx++;
while (idx < _ht->_tables.size())
{
if (_ht->_tables[idx] != nullptr)
{
_node = _ht->_tables[idx];
break;
}
else
{
idx++;
}
}

if (idx == _ht->_tables.size())
{
_node = nullptr;
}
}
return *this;
}
const HT* _ht;
const Node* _node;
};

template <class K, class T, class GetKey, class KeyOfT>
class HashTable
{
typedef HashNode<T> Node;

template<class K, class T, class GetKey, class KeyOfT>
friend struct HashIterator;// 迭代器需要访问私有

template <class K, class T, class Hash, class KeyOfT>
friend struct ConstHashIterator;

public:
typedef HashIterator<K, T, GetKey, KeyOfT> iterator;
typedef ConstHashIterator<K, T, GetKey, KeyOfT> const_iterator;
iterator begin()
{
for (size_t i = 0; i < _tables.size(); i++)
{
if (_tables[i])
{
return iterator(this, _tables[i]);
}
}
return iterator(this, nullptr);
}

iterator end()
{
return iterator(this, nullptr);
}

const_iterator cbegin()
{
for (size_t i = 0; i < _tables.size(); i++)
{
if (_tables[i])
{
return const_iterator(this, _tables[i]);
}
}
return const_iterator(this, nullptr);
}

const_iterator cend()
{
return const_iterator(this, nullptr);
}

HashTable()
: _n(0)
{
_tables.resize(10);
}

~HashTable()
{
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}

pair<iterator, bool> insert(const T& data)
{
// 重复
iterator it = find(KeyOfT()(data));
if (it != end())
{
return make_pair(it, false);
}
// 负载因子为1扩容
if (_tables.size() == _n)
{
vector<Node*> newtable;
newtable.resize(2 * _n);
for (size_t i = 0; i < _tables.size(); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t idx = GetKey()(KeyOfT()(data)) % newtable.size();
cur->_next = newtable[idx];
newtable[idx] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newtable);
}

size_t hashI = GetKey()(KeyOfT()(data)) % _tables.size();
Node* newnode = new Node(data);
newnode->_next = _tables[hashI];
_tables[hashI] = newnode;
++_n;
return make_pair(iterator(this, newnode), true);
}

iterator find(const K& key)
{
size_t idx = GetKey()(key) % _tables.size();
Node* cur = _tables[idx];
while (cur)
{
if (KeyOfT()(cur->_data) == key)
return iterator(this, cur);
else
cur = cur->_next;
}
return end();
}

bool erase(const K& key)
{
size_t idx = GetKey()(KeyOfT()(key)) % _tables.size();
Node* cur = _tables[idx];
Node* pre = nullptr;
while (cur)
{
if (cur->_data == key)
{
if (pre = nullptr)
{
_tables[idx] = nullptr;
}
else
{
pre->_next = cur->_next;
}
delete cur;
--_n;
return true;
}
else
{
pre = cur;
cur = cur->_next;
}
}
return false;
}
private:
vector<Node*> _tables;
size_t _n = 0;
};
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334