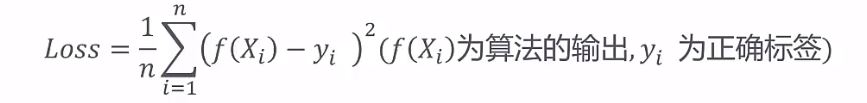@机器学习
什么是机器学习
机器学习(Machine Learning, ML)是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。
它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域,它主要使用归纳、综合而不是演绎
简单来说机器学习就是机器学习是用数据或以往的经验,以此优化计算机程序的性能标准。从数据中挖掘潜在的规律,以便在下次遇到相似的数据时能够进行分析,就好像我们做大量练习题一样来巩固知识点和知识点之间的联系,以便我们在高考的时候取得更好的成绩
机器学习-输入
基本概念:
1、特征向量:X=(x1,x2,…,xN)
简单来说就是特征的集合,描绘了一个我们研究的对象
比如我们要描述一个人,那么我们就要用到身高,体重,肤色,工作等特征,我们把这些特征放入一个向量中就构成了我们所说的特征向量,特征向量有多个维度,每个维度代表特征向量的取值,就像数据库中的一张表
2、标签:{y|y属于{-1,0,1,2}}
表示特征向量所属的类别
如上述例子,人分为好人坏人,好人坏人就是人的标签,特征向量和标签是成对出现的,映射在数学意义上可以用0和1表示,当标签未知可以用-1表示,标签一般从0开始
3、数据集:特征向量和标签的集合s={(X1,y1),(X2,y2),…}
数据集分类:
1)训练集:用于建立模型,是输入到算法的主体,算法是从训练集中学习规律的
2)验证集:用来检验中间选择最优的模型的性能如何,是在训练的过程中使用的,算法的学习是循环迭代的,在学习的某个时间点,算法会在验证集上进行测试,测试当前算法的效果,然后根据测试结果对算法训练的行为进行一系列的调整,这调整可能是算法内部的调整也可以是认为的调整,说白了就像月考,对一个阶段的学习进行评估,进而进行下一步的学习。
注意测试集并不是每个算法都必须有的
3)测试集:用来检验最终选择最优的模型的性能如何
就好像高考,前面的学习都是为了高考的时候一发冲天
机器学习-输出
给定输入的特征向量X,特定的算法经过计算,输出对应的标签y
机器学习的目标与评价
就和我们平常做作业全对,但在考试的时候都是红叉叉,这样学习效果是不好的,我们希望平时做作业全对,最后考试的时候也能全对。
对机器学习的评价,例如回归任务通常使用均方误差来衡量算法的效果
loss越小算法输出越接近正确标签,算法的效果也就越好
经验风险最小化
经验风险最小化是上面不同评价方法的基本指导原则
算法并不能提前知道数据的真实分布,我们需要作出假设来表示训练完的算法在真实的数据集上的表现,首先训练集是真实数据集的一个缩影,训练集上的误差是可以计算的,那么我们就可以通过最小化训练集上的误差来最小化真实集上的误差。这就是经验风险最小化
注:前提是训练集必须最能完整的反映真实集
千万不要我们学着电磁学而考试考的是动力学
过拟合与欠拟合
过拟合(over-fitting)其实就是所建的机器学习模型或者是深度学习模型在训练样本中表现得过于优越,导致在验证数据集以及测试数据集中表现不佳。欠拟合则是在训练集上表现就不好,导致在测试集上表现也不好,就好比下面这张图
详细大白话可看:https://blog.csdn.net/qq_18254385/article/details/78428887
归纳偏置
归纳偏置:
机器学习试图去建造一个可以学习的算法,用来预测某个目标的结果。要达到此目的,要给于学习算法一些训练样本,样本说明输入与输出之间的预期关系。然后假设学习器在预测中逼近正确的结果,其中包括在训练中未出现的样本。既然未知状况可以是任意的结果,若没有其它额外的假设,这任务就无法解决。这种关于目标函数的必要假设就称为归纳偏置
简洁明了的说就是事先对机器学习算法的一种假设、一种偏好,从概率论的角度来看,归纳偏置是加入到算法中的先验信息
作用
- 减少搜索空间
- 减缓过拟合
用下面的图例说明,
任务是要找到你和较好的回归模型,第一幅图我们事先假设回归模型是线性模型,那么线性模型就是我们的归纳偏置
拿我们做一个数学几何题来说,我们做题都要事先假设是考察我们哪方面的知识,我们用平面几何来解题,平面几何就是我们的归纳偏置。当然只有归纳偏置是合理的我们才能得到正确结果
以下是机器学习中常见的归纳偏置列表:
最大条件独立性(conditional independence):如果假说能转成贝叶斯模型架构,则试着使用最大化条件独立性。这是用于朴素贝叶斯分类器(Naive Bayes classifier)的偏置。
最小交叉验证误差:当试图在假说中做选择时,挑选那个具有最低交叉验证误差的假说,虽然交叉验证看起来可能无关偏置,但天下没有免费的午餐理论显示交叉验证已是偏置的。
最大边界:当要在两个类别间画一道分界线时,试图去最大化边界的宽度。这是用于支持向量机的偏置,它假设不同的类别是由宽界线来区分。
最小描述长度(Minimum description length):当构成一个假设时,试图去最小化其假设的描述长度。假设越简单,越可能为真的。见奥卡姆剃刀。
最少特征数(Minimum features):除非有充分的证据显示一个特征是有效用的,否则它应当被删除。这是特征选择(feature selection)算法背后所使用的假设。
最近邻居:假设在特征空间(feature space)中一小区域内大部分的样本是同属一类。给一个未知类别的样本,猜测它与它最紧接的大部分邻居是同属一类。这是用于最近邻居法的偏置。这个假设是相近的样本应倾向同属于一类别。 [1]
独立同分布条件
独立同分布条件(i.id条件)
定义:训练集和测试集是从同一个数据分布中抽取的,并且抽取的过程是独立的(independent and identically distributed)
只有满足独立同分布条件,前面我们所说的经验最小化才是成立的。
独立同分布条件-推论
1、数据集越大,月能真实反映数据的真实分布(ImageNet竞赛的训练集的图片有数百万张)
2.数据集的质量很重要(比如我们做练习题要做不同类型的,而不是制作一个类型,这样我们考试的时候才能灵活运用学习到的知识,在考试中取得一个好成绩)