前言

        无论你是计算机科学专业的学生、程序设计的爱好者，还是正在准备面试的求职者，本文将为你提供一份全面而深入的栈和队列指南。让我们一起探索栈和队列的双重魅力，为你的编程之路增添新的色彩。

1. 栈

1.1栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。

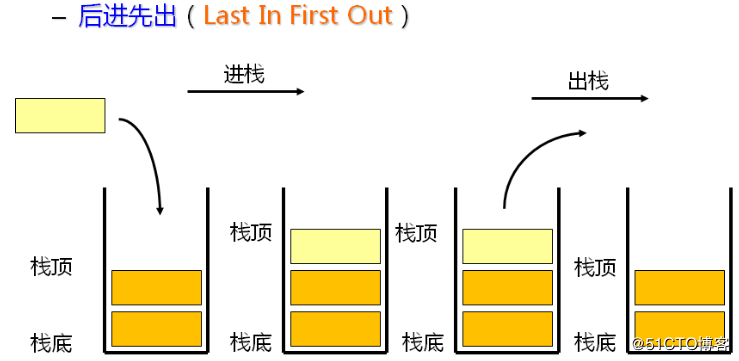
栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

• 压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
• 出栈：栈的删除操作叫做出栈。出数据也在栈顶。

 1.2 栈的实现

        栈的实现方法有两种，一种是顺序表的栈，另外一种就是链表实现的栈。相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小，所以这里我们使用顺序表来实现栈。

         如果熟练顺序表和链表操作，那栈就会相当轻松，栈的入栈出栈就相当于是尾插尾删，顺序表尾插尾删的效率高，这也是使用顺序表实现的原因。

1.2.1 栈的定义

首先我们需要先定义一个栈：

typedef int Datatype;
typedef struct Stack
{
Datatype* a;
int top;
int capacity;
}Stack;

 栈中有栈顶（top），有栈的容量（size），还有存储的数据（a）；

 1.2.2  栈的初始化

void InItStack(Stack* ps)
{
assert(ps);
ps->top = 0;
ps->a = NULL;
ps->capacity = 0;
}

         这里对栈进行初始化时栈顶（top）可以置为-1，也可以置为0，置为0为了便于使用top作为数组下标插入数据。

1.2.3 入栈

        栈已经定义完成并且进行了初始化，接下来就是入栈操作。这里与顺序表的尾插略微有些不同。

void StackPush(Stack* ps, Datatype x)
{
assert(ps);
if (ps->top == ps->capacity)
{
int newcapacity = (ps->capacity == 0 ? 4 : ps->capacity * 2);
Datatype* tmp = (Datatype*)realloc(ps->a, sizeof(Datatype) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->capacity = newcapacity;
}
ps->a[ps->top] = x;//top初始化为0，可以直接作为数组下标
ps->top++;//入栈后top++，便于统计元素个数和下次入栈
}

        由于我们初始化时将栈的容量置为0，在这里我们在入栈操作时就需要进行开辟空间，但这里如果我们使用malloc开辟空间，就还需要进行扩容操作，所以我们直接使用realloc进行开辟空间。

 realloc在扩容时，如果原始区域空间为0，那么它的作用就类似于malloc。

         此外我们还需要有新开辟空间的大小，这里我们直接使用一个判断语句：newsize = (ps->size == 0 ? 4 : ps->size * 2);  如果size等于0就开辟4个存储数据的空间，如果不等于0就直接扩容为2倍。

1.2.4 出栈

 出栈操作就很简单了，也不需要销毁，直接进行top--：

void StackPop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}

        但我们需要注意栈为空的情况，所有使用assert强制检查，如果为空直接报错终止程序，简单粗暴。

1.2.5  栈的元素个数

统计栈的元素个数接口也很简单，top就是栈中元素的个数

int Stacksize(Stack* ps)
{
assert(ps);
return ps->top;
}

1.2.6 栈顶数据

Datatype TopData(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
 
return ps->a[ps->top - 1];
}

这个也非常简单，需要注意栈为空的情况。

1.2.7 栈的判空

bool IsEmpty(Stack* ps)
{
assert(ps);
return (ps->top == 0);
}

 2.栈的应用

         这些栈的基本操作我们已经实现了，接下来我们来实际应用一下。虽然栈的基本操作更为简单，但是栈在应用时数据的结构更加复杂，前边的顺序表和链表是栈和队列的基础。

 2.1 题目一：括号匹配

        这道题目我们可以使用数组实现并解决，但我们已经了解了栈，这道题目我们就使用顺序表栈来实现。我们可以直接复制上述栈基本操作的代码。将 typedef  int  Datatype;

 改为：typedef  char  Datatype;

题目描述：

 示例：

 题目链接：

有效括号

2.1.1 思路

         这道题目的思路很明确，入栈左括号，遇到匹配的右括号就出栈。如果最终栈为空就匹配成功。但匹配失败的情况有很多，接下来我们进行逐个分析。

 2.1.2 分析

         首先是入栈，如果为左括号就入栈，为右括号就匹配出栈。这里使用if…else语句更为简洁，入栈就需要我们调用入栈的函数接口。

        其次就是匹配、出栈。但在匹配之前我们还需要考虑特殊情况，就是如果没有出栈元素就直接匹配的情况，所以首先我们需要有一个判空操作，如果匹配时栈就为空就直接匹配失败，并销毁栈，这个属于左括号与右括号数量匹配失败。

         接着就是顺序匹配失败，这里就需要我们用到栈顶元素了，如果栈顶元素与匹配的括号不匹配就直接返回false，匹配失败，销毁栈。

        最后，匹配结束，存放括号数组为空，栈也为空就匹配成功。

 2.1.3 题解

匹配括号接口：

bool isValid(char* s) {
Stack st;
InItStack(&st);
char top;
while (*s)
{
if (*s == '(' || *s == '[' || *s == '{')
{
StackPush(&st, *s);
}
else
{
if(IsEmpty(&st))
{
DestoryStack(&st);
return false;
}
top=TopData(&st);
StackPop(&st);
if((*s==']'&&top!='[')
||(*s==')'&&top!='(')
||(*s=='}'&&top!='{'))
            {
                DestoryStack(&st);
                return false;
            }
}
        s++;
}
bool ret = IsEmpty(&st);
    DestoryStack(&st);
return ret;
}

整体代码：

typedef char Datatype;
typedef struct Stack
{
Datatype* a;
int top;
int size;
}Stack;
 
void InItStack(Stack* ps);
 
void DestoryStack(Stack* ps);
 
void StackPush(Stack* ps, Datatype x);
 
void StackPop(Stack* ps);
 
int Stacksize(Stack* ps);
 
Datatype TopData(Stack* ps);
 
bool IsEmpty(Stack* ps);
 
void InItStack(Stack* ps)
{
assert(ps);
ps->top = 0;
ps->a = NULL;
ps->size = 0;
}
 
void DestoryStack(Stack* ps)
{
assert(ps);
ps->top = ps->size = 0;
free(ps->a);
ps->a = NULL;
}
void StackPush(Stack* ps, Datatype x)
{
assert(ps);
if (ps->top == ps->size)
{
int newsize = (ps->size == 0 ? 4 : ps->size * 2);
Datatype* tmp = (Datatype*)realloc(ps->a, sizeof(Datatype) * newsize);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->size = newsize;
}
ps->a[ps->top] = x;
ps->top++;
}
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
int Stacksize(Stack* ps)
{
assert(ps);
return ps->top;
}
Datatype TopData(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
 
return ps->a[ps->top - 1];
}
bool IsEmpty(Stack* ps)
{
assert(ps);
return (ps->top == 0);
}
bool isValid(char* s) {
Stack st;
InItStack(&st);
char top;
while (*s)
{
if (*s == '(' || *s == '[' || *s == '{')
{
StackPush(&st, *s);
}
else
{
if(IsEmpty(&st))
{
DestoryStack(&st);
return false;
}
top=TopData(&st);
StackPop(&st);
if((*s==']'&&top!='[')
||(*s==')'&&top!='(')
||(*s=='}'&&top!='{'))
            {
                DestoryStack(&st);
                return false;
            }
}
        s++;
}
bool ret = IsEmpty(&st);
    DestoryStack(&st);
return ret;
}

         栈相对于链表和顺序表没有那么多的操作，更为简单，但在实际应用时数据结构更加复杂，但是别担心，后续学习C++后可以直接使用现成的库函数，不需要再对栈的各个操作进行实现。

总结

        栈是一种重要的数据结构，它以后进先出的方式操作数据。栈在递归算法、表达式求值、函数调用等场景中发挥着重要作用。通过学习栈，我们能够更好地理解数据结构的本质和算法的设计思想。栈不仅仅是一种数据存储的方式，更是一种思维方式和问题解决的工具。无论是计算机科学的学习者、程序设计的爱好者，还是正在准备面试的求职者，通过探索栈的原理和应用，我们能够提升自己的编程能力和解决问题的能力。让我们一起深入探索栈的魅力，为编程之路增添新的色彩。最后，感谢阅读！