一、问题描述

旅行商问题是指旅行家要旅行n个城市，要求每个城市经历一次且仅经历一次然后回到出发城市，并要求所走路程最短。

首先通过所给出的一个无向图，即n个顶点，m个无向边，每条边有一个权值代表两个点之间的距离，要求把每一个点都走一遍并回到原点，求路径的最短值。

二、问题分析

（1）分析：从初始点出发的周游路线一共有(n-1)!条，即等于除初始结点外的n-1个结点的排列数，因此旅行商问题是一个排列问题。通过枚举(n-1)!条周游路线，从中找出一条具有最小成本的周游路线的算法，其计算时间为O(n!)。

（2）完成方案：可以通过将问题给出的无向图，如：图1，即城市点和到其他城市的所需路程集合成一个二维数组，且保证到自身的路程设置为无穷大避免方案中出现到原本所在城市的方案，如：图2。再通过动态规划、贪心法、分支限界等算法进行相应算法的求解。

（3）预期结果：在程序运行后显示最佳方案的结果。

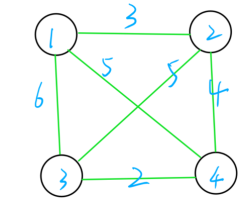
图1 无向图

图2 无向图对应的矩阵

三、算法设计与分析

1、算法输入和输出

（1）算法输入：城市数量，到其他城市的距离（到自身距离设置为无穷大）；

（2）算法输出：路过所有城市所需总路径的最小值

2、算法说明

（1）贪心法：贪心算法总是作出在当前看来最好的选择。贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。虽然贪心算法不能对所有问题都得到整体最优解，但对许多问题它能产生整体最优解。例如单源最短路经问题，最小生成树问题等。在一些情况下，即使贪心算法不能得到整体最优解，其最终结果却是最优解的很好近似。

（2）动态规划法：动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题；但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。

（3）分支限界法：分支限界法：采用广度优先产生状态空间树的结点，并使用剪枝函数的方法。“分支”采用广度优先策略，依次生成扩展结点的所有分支（即，儿子结点）。

“限界”在结点的扩展过程中，计算结点的上界（或下界），边搜索边剪枝，以提高搜索效率。

3、算法描述

（1）贪心法：采用最近邻点策略，从任意一点出发，每次到没经过的点中最近的一个，直到经过所有的点，最后回到出发点。即如果当前在顶点u，则取与顶点u距离最近的点p。

（2）动态规划法：某一个点i不经过任意点回到起始点的最短路径和为mp[i][0](默认初始点为0)，dp[i][0]= mp[i][0];(1<=i<n)。点i经过集合S（二进制表示的数为j）的最短路径和为从点i经过集合S中的某一点k后再从该点出发，经过集合S-{k}的最小值。dp[i][j]=min{mp[i][k]+dp[k][j-(1<<(k-1))};

（3）分支限界法：首先通过贪心法求解的值作为上界，把每个点最近的两条边之和的1/2作为下界。分支限界法通过设定目标函数，每次从优先级队列中取目标函数的值最小的节点。先判断是否已经经过了n-1个点，如果已经经过了n-1个点，那么可直接求出最短路径和，并与在队列里的其他节点的目标函数值比较，如果该路径和比其他所有在队列里的节点的目标函数值都小，那么改路径和就是问题的解。否则，继续计算优先级队列里面的其他节点。

4、算法分析

（1）贪心法：从起始点开始，每次寻找未经过的点中距离当前点最近的点，作为下一步要遍历的点，直到所有点遍历完，回到起始点。适用于求上界。

（2）动态规划法：假设从顶点s出发，令d(i, V’)表示从顶点i出发经过V’(是一个点的集合)中各个顶点一次且仅一次，最后回到出发点s的最短路径长度。适用于求少城市。

（3）分支限界法：首先定义节点结构，优先级队列，存储图的邻接矩阵，并读入数据。计算每个城市的最小距离，以及所有城市的最小距离之和。从初始节点开始遍历，搜索排列空间树。取出节点并进行扩展，如果遇到了叶子节点的父节点，尝试更新最优解，遇到了叶子节点则结束遍历。从叶子节点得到最优解的路径。适用于求多城市。

四、算法流程图

（1）贪心法：见下图3。

图3 贪心法算法流程图

（2）动态规划法：见下图4。

图4 动态规划法算法流程图

（3）分支限界法：见下图5。

图5 分支限界法算法流程图

五、测试数据及其结果分析

（1）贪心法：测试数据如下代码所示，运行结果如图6所示。

分析：先通过 visit 函数来判断是否经过城市，然后通过 clostCityDistance 函数查找距离当前城市最近的下一个城市，最后通过 TSP 函数来求和输出。

图6 贪心法运行结果

#include<iostream>
#define n 4
using namespace std;
int s[n] = { -1,-1,-1,-1 };// 记录已经访问过的城市, 初始化为-1,表示未访问
int distance[n][n] = { {10000,3,6,5},// 城市间距离数组,10000表示自己到自己的距离
                      {3,10000,5,4},
                      {6,5,10000,2},
                      {5,4,2,10000} };
bool visit(int k) {//判断城市k是否被访问过 
    for (int i = 0; i < n; i++)
        if (s[i] == k) return 1;
    return 0;
}
 
void clostCityDistance(int currentCity) { //查找距离当前城市最近的下一个城市       
    int Dtemp = 10000;//Dtemp暂时存储当前最小路径的值 
    for (int i = 0; i < n; i++)
    {
        if (visit(i) == 0 && ::distance[i][s[currentCity]] < Dtemp)
        {
            Dtemp = ::distance[i][s[currentCity]];
            s[currentCity + 1] = i;
//若该城市没有被访问过，且距离当前城市最短，则将访问该城市，存入s[]数组中 
        }
    }
 
    for (int i = 0; i < n; i++)
    {//查找是否还有未访问的城市 
        if (s[i] == -1)
            clostCityDistance(s[currentCity + 1]);
    }
}
void TSP() {
    int sum = 0;// 最短路径之和 
    s[0] = 2;//从第2个城市出发 ，初始化出发的城市,可在0,1,2,3中任意一个 
    clostCityDistance(s[0]);//寻找距离2城市最近的城市   
    for (int i = 0; i < n; i++) {
        if (i == n - 1) {
            printf("%d", s[i]);
            printf("->%d 距离为：%d\n", s[0], ::distance[s[n - 1]][s[0]]);
            printf("总距离是  %d\n", sum += ::distance[s[n - 1]][s[0]]);
            break;
        }
        printf("%d->%d 距离为：%d \n", s[i], s[i + 1], ::distance[s[i]][s[i + 1]]);
        sum += ::distance[s[i]][s[i + 1]];
    }
}
int main() {
    TSP();
    return 0;
}

（2）动态规划法：测试数据如下代码所示，运行结果如图7所示。

分析：先通过 Tsp tsp(city_number) 函数来初始化二维矩阵，然后通过 tsp.printCity函数打印城市，再通过 tsp.printProcess函数来计算，最后通过 tsp.getShoretstDistance函数来求最短路径。

图7 动态规划法运行结果

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
#define MAX_IN 10
 
class Tsp
{
private:
    int city_number;        //城市个数
    int** distance;            //城市距离矩阵
    int** process;            //求最短路径的过程矩阵
public:
    Tsp(int city_number);        //构造函数
    void correct();            //矫正输入的城市代价矩阵
    void printCity();        //打印城市的距离矩阵
    void getShoretstDistance();    //动态规划法求最短路径
    void printProcess();        //打印过程矩阵
 
};
 
//构造函数
Tsp::Tsp(int city_num)
{
    int i = 0, j = 0;
    city_number = city_num;
 
    //初始化城市距离矩阵
    distance = new int* [city_number];
    cout << "请输入" << city_number << "个城市之间的距离" << endl;
    for (i = 0; i < city_number; i++)
    {
        distance[i] = new int[city_number];
        for (j = 0; j < city_number; j++)
            cin >> distance[i][j];
    }
 
    //生成过程矩阵
    process = new int* [city_number];
    for (i = 0; i < city_number; i++)
    {
        process[i] = new int[1 << (city_number - 1)];
    }
 
 
}
 
//纠正用户输入的城市代价矩阵
void Tsp::correct()
{
    int i;
    for (i = 0; i < city_number; i++)
    {
        distance[i][i] = 0;
    }
}
 
//打印城市距离
void Tsp::printCity()
{
    int i, j;
    //打印代价矩阵
    cout << "您输入的城市距离如下" << endl;
    for (i = 0; i < city_number; i++)
    {
        for (j = 0; j < city_number; j++)
            cout << setw(3) << distance[i][j];
        cout << endl;
    }
}
 
//动态规划法求最短路径
void Tsp::getShoretstDistance()
{
    int i, j, k;
    //初始化第一列
    for (i = 0; i < city_number; i++)
    {
        process[i][0] = distance[i][0];
    }
    //初始化剩余列
    for (j = 1; j < (1 << (city_number - 1)); j++)
    {
        for (i = 0; i < city_number; i++)
        {
            process[i][j] = 0x7ffff;//设0x7ffff为无穷大
 
            //对于数字x，要看它的第i位是不是1，通过判断布尔表达式 (((x >> (i - 1) ) & 1) == 1的真值来实现
 
            if (((j >> (i - 1)) & 1) == 1)
            {
                continue;
            }
            for (k = 1; k < city_number; k++)
            {
                //不能达到k城市
                if (((j >> (k - 1)) & 1) == 0)
                {
                    continue;
                }
                if (process[i][j] > distance[i][k] + process[k][j ^ (1 << (k - 1))])
                {
                    process[i][j] = distance[i][k] + process[k][j ^ (1 << (k - 1))];
                    //cout<<i<<"行"<<j<<"列为："<<process[i][j]<<endl;
                }
            }
        }
    }
    cout << "最短路径为" << process[0][(1 << (city_number - 1)) - 1] << endl;
}
//打印过程矩阵
void Tsp::printProcess()
{
    int i, j;
    for (j = 0; j < 1 << (city_number - 1); j++)
    {
        cout << setw(3) << j;
    }
    cout << endl;
    for (i = 0; i < city_number; i++)
    {
        for (j = 0; j < 1 << (city_number - 1); j++)
        {
            if (process[i][j] == 0x7ffff)
                process[i][j] = -1;
            cout << setw(3) << process[i][j];
        }
        cout << endl;
 
    }
}
//主函数
int main(void)
{
    int city_number;
    while (cin >> city_number)
    {
        Tsp tsp(city_number);        //初始化城市代价矩阵
        tsp.correct();                    //纠正用户输入的代价矩阵
        tsp.printCity();                //打印城市
        tsp.getShoretstDistance();        //求出最短路径
        tsp.printProcess();            //打印计算矩阵
    }
    return 0;
}

（3）分支限界法：测试数据如下代码所示，运行结果如图8所示。

分析：先通过 main 函数来初始化二维矩阵，然后通过 Traveling函数计算行程路径及最短路径，最后通过 print函数来打印最短路径。

图8 分支限界法运行结果

#include<iostream>
using namespace std;
#define NoEdge -1
#define MAX 20
int G[MAX][MAX];
int ans[MAX], x[MAX];
int bestc, cc;
void init(int n)
{
    int i, j, len;
    memset(G, NoEdge, sizeof(G));
    while (cin >> i >> j)
    {
        if (i == 0 && j == 0) break;cin >> len;
 
        G[i][j] = len;
        G[j][i] = len;
}
    for (i = 1;i <= n;i++) x[i] = i;bestc = 0x7fffff;
 
    cc = 0;
}
void Swap(int& i, int& j)
{
    int t = i;
    i = j;
    j = t;
}
void Traveling(int i, int n)
{
    int j;
 
    if (i == n + 1)
    {
        if (G[x[n - 1]][x[n]] != NoEdge && G[x[n]][1] != NoEdge && (cc + G[x[n]][1] < bestc))
        {
            for (j = 1;j <= n;j++)ans[j] = x[j];
 
            bestc = cc += G[x[n]][1];
        }
    }
    else {
        for (j = i;j <= n;j++) {
 
            if (G[x[i - 1]][x[j]] != NoEdge && (cc + G[x[i - 1]][x[j]] < bestc))
            {
                Swap(x[i], x[j]);
 
                cc += G[x[i - 1]][x[i]];Traveling(i + 1, n);cc -= G[x[i - 1]][x[i]];Swap(x[i], x[j]);
            }
        }
    }
}
void print(int n)
{
    cout << "最小的旅行费用为: " << bestc << endl;
    cout << "最佳路径是: ";
    for (int i = 1;i <= n;i++)
        cout << ans[i] << "->";
    cout << ans[1] << endl;
}
int main()
{
    int n;
 
    cout << "请输人需要旅行多少个城市: " << endl;
    while (cin >> n && n) {
 
        cout << "輸人丙个城市之同的距高，例如1 2 20,輸人00結束" << endl;
        init(n);
        Traveling(2, n);
        print(n);
    }
    return 0;