一、调节变量
根据侯杰泰 等(2004)的研究,如果变量Y和变量X的关系是变量M的函数 (Y=f(X,M)+e) ,即Y和X的关系受到第三个变量M的影响,则称M为调节变量。调节变量可以是定性的(如性别、种族、学校类型等),也可以是定量的(如年龄、受教育程度等),它影响因变量和自变量之间关系的强弱。
举一个栗子,不妨以员工的工作压力为自变量,员工的离职倾向为因变量,员工工资为调节变量。当员工工作压力越大,员工的离职倾向越强,二者呈正向因果关系;调节变量的弱化作用体现为:①高员工工资能够弱化二者的正向因果关系,即当员工工资变高,工作压力高的员工离职倾向可能变弱;调节变量的强化作用体现为:②低员工工资能够强化二者的正向因果关系,即当员工工资降低,工作压力高的员工离职倾向可能变弱。
二、调节效应检验方法
回顾之前的文章,不难发现中介效应的检验共包含三个方法,分别是:①依次检验回归系数 ②PROCESS插件方法③Amos结构方程分析方法。同样地,调节效应的检验也有同样的三种方法。本文首先介绍方法一,即依次检验回归系数的方法,该方法主要应用到的工具为SPSS23.0。
在探究如何检验调节效应之前,我们首先需要明白:调节效应检验=检验交互项显著性≠检验调节变量显著性!!!
三、调节效应检验步骤
依次检验回归系数的方法我们参考侯杰泰 等(2004)学者的研究成果(表1)。
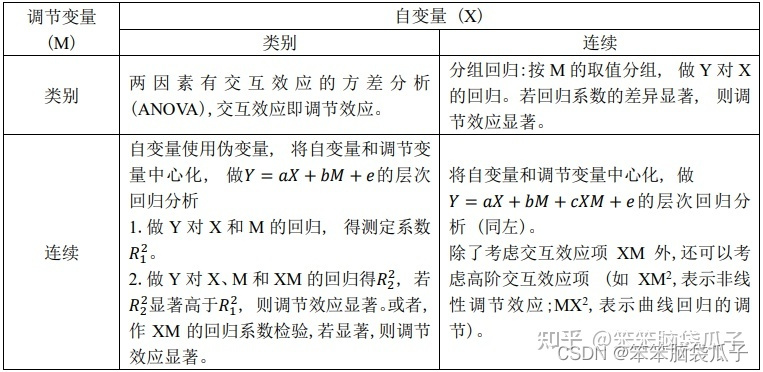
首先我们构建两大方程如下:
方程一: Y=aX+bM+e
方程二: Y=aX+bM+cXM+e
方法的原理在于,比对两个模型的 R12 与 R22 ,如果二者差异显著,则表示加入交互项X*M后,对因变量的预测结果发生了显著变化,则意味着调节效应显著。再次强调:调节效应检验=检验交互项显著性≠检验调节变量显著性!!!我们关注的始终是交互项在自变量与因变量关系上的作用,是交互项与因变量的关系,而非调节变量与因变量的关系。
1. 操作步骤
不妨假设自变量为员工工作压力WA,工作压力由8个测量题项测量;因变量为离职倾向TI,离职倾向由9个测量题项测量;调节变量为组织支持感PO,组织支持感由6个测量题项测量(图1)。

第一步:自变量与调节变量中心化/标准化
在前面的文章《数据中心化与标准化》中,我们已经介绍过如何进行变量中心化,具体可以参考该文章。
打开SPSS 23.0→数据→拖入自变量与调节变量的题项至变量摘要栏→确定→计算各个题项的均值
转换→计算变量→输入公式((题项1-题项1均值)+ (题项2-题项2均值)+……+(题项i-题项i均值))/i→由此得到中心化后的自变量ZWA与调节变量ZPO

第二步:计算交互项
转换→计算变量→输入公式ZWA*ZPO→得到交互项int1 
第三步:层级回归分析
分析→回归→线性→在第一层自变量栏输入中心化后的自变量ZWA与调节变量ZPO→在第二层自变量栏输入中心化后的自变量ZWA、调节变量ZPO与交互项int1→Statistics(统计)→勾选R方变化(该值用于检验调节效应是否显著)→勾选共线性诊断(该值用于判断自变量之间是否存在严重的多重共线性问题)→勾选Durbin-Watson(该值用于判断残差是否存在严重的自相关问题)→确定
2. 结果
第一步:调节效应检验
由模型摘要(表2),我们主要查看“R平方”“显著性F值变更”“Durbin-Watson”三个值,R平方代表自变量对因变量的解释率,例如在模型1中,自变量WA与调节变量PO对因变量TI的解释率为7.7%,而模型2中,自变量WA、调节变量PO与交互项int1对因变量TI的解释率为8.1%。“显著性F值变更”反映的是R平方的变化是否显著,由模型2的“显著性F值变更”为0.037<0.05,意味着调节效应显著。


由表3的模型2,自变量ZWA( p=0.002<0.01)、调节变量ZPO( p=0.000<0.01)与交互项int1( p=0.037<0.05 )对因变量TI的影响显著( p<0.05),故调节效应显著。
第二步:多重共线性与自相关问题判断
一般而言,VIF值大于1,越接近1多重共线性弱,越大代表多重共线性强;若VIF>10,则存在严重的多重共线性问题(范立新,1994)。由表3,模型的VIF值(方差膨胀因子,即容忍度的倒数)介于1.039~1.207之间,不存在严重的多重共线性问题。
自相关问题通过DW值判断,DW值一般介于0~4之间,当DW=2,则意味着残差序列没有自相关问题,因此粗略而言,只要检验DW值接近2即可。
由表2,DW=1.720,接近2,不存在严重的自相关问题。
参考文献
[1]温忠麟,侯杰泰,张雷.调节效应与中介效应的比较和应用[J].心理学报,2005(02):268-274.
[2]范立新.回归分析中多重共线性诊断方法[J].国外医学.卫生学分册,1994(01):34-37.
[3]刘明,王永瑜.Durbin-Watson自相关检验应用问题探讨[J].数量经济技术经济研究,2014,31(06):153-160.