重复测量资料纵向研究的数据分析-1
单变量组内设计
在纵向研究中,如果对同一个体的测量次数超过两次,情况会变得比较复杂。配对t检验就不再适用。
先来理解什么是“单变量组内设计(One-within design)”,只有一个结果变量,且在同一组个体中进行多次测量。研究组内结果变量随时间的变化情况。
一、分析方法
1.多元方差分析(多变量分析)
多元方差分析(Multivariate analysis of variance,MANOVA),又称重复测量资料的广义线性模型(Generalized linear model(GLM)for repeated measures)可分析结果变量Y随时间变化而变化的问题。
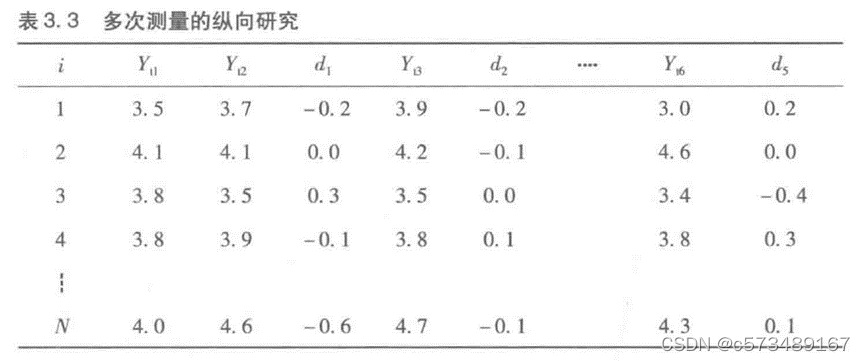
MANOVA基本统计思想与配对t检验是相同的。T次测量可得到出T-1个差值(前一次减后一次),比较T-1个差值的方差分析结果。多元是指将T-1个差值同时作为结果变量。统计检验方法是基于T-1个差值及所对应的方差、协方差。F统计量是服从自由度为(T-1),(N-T+1)的F分布(F-distribution)。
MANOVA的基本假设与配对t检验有一定可比性:(1)独立(每个个体的每次测量结果是独立的);(2)正态分布(每个个体测量所得到的的观测数据服从正态分布)。
2.单变量分析(univariate)
单变量分析与一般方差分析具有相似性(误差的分解)。需满足于多元方差分析的条件外,还需满足球形假设(Sphericity Assumed),又称复合对称性假设(Compound symmtery)。多次重复测量所得的Y值之间的相关性相等,且方差一致。球形度系数(Sphericy coefficient)ε=1,数据结构符合。
二、结果解读
1.多变量分析结果

结果变量Y,重复测量6次(t=1~6),探索Y在t=1和t=6之间,是否随时间变化而变化。F值和显著性水平是基于多变量检验(Multivariate test)的结果。总体时间效应显著(p=0.000),即结果变量Y随时间而变化。分析方法是用提出该方法的统计学家名字命名,分析过程中存在的差异较小,最后结果基本一致。
2.球形检验

通过Greenhouse-Geisser的方法得到球形度系数ε为0.741,通过Mauchly的球形检验可以得到ε的显著性。结果显示拒绝原假设(p=0.000),即球形假设不满足。需要对F检验进行自由度校正(自动校正)。
3.单变量分析结果

个体内效应检验(Tests of Within-Subject effects)为单变量分析结果。时间效应估计(time),第一个是球形假设(Sphericity Assumed),其他三种(Greenhouse-Geisser、Huynh-Feldt、Lower-bound)是在球形假设不满足的情况下,自由度校正方法。推荐使用Greenhouse-Geisser,方法相对保守。结论是随时间变化结果变量Y变化显著。具体的变化情况,需进行函数关系检验。
3.函数关系检验

从个体内差异(Tests of Within-Subjects Contrasts)结果得到线性检验的结果(Linear),F=126.240,p=0.000,表明结果变量与时间可能存在线性关系。Quadratic(二次)、Cubic(三次)等都显著。Y与时间存在某种关系,具体关系如何呢?结果变量随时间的变化增加了还是减少了需作图,才能更好的解释分析结果。
4.绘图

边际均值:样本在每个测量时间的均值。
图示结果显示,变化趋势是小幅度减少,然后迅速增加。
5.时间效应强度

以上分析可知,结果变量Y与时间存在一定的关系,Y随时间变化会发生变化,那么变化的强度是怎么样的?时间效应强度(Strength of effect)大小可以用η2 (eta square)表示,即特定效应平方和与总平方和的比值。表示变量Y的变化有多少可通过时间效应来解释。eta square=0.406(89.99/(131.40+89.99))。时间效应解释了结果变量Y的41%的方差。
三、总结
1.重复测量资料的方差分析的理解
在不考虑每个个体重复测量做数据之间的非独立性,只是在6次测量之间比较结果变量Y的均值。(此方法为常规意义上的方差分析,若仅有两次,则与两独立样本t检验和配对样本t检验一样)。常规的方差分析显示F=32.199,P=0,000,结果显示至少有一个时间点的结果变量Y的均值与其他的某一个时间点的结果变量Y的均值相比有显著性差异。
但是纵向研究的本质是同一个体在不同时间点被重复测量,数据之间是不独立的。所以MANOVA与ANOVA是有差别的。ANOVA的误差平方和远大于MANOVA的误差平方和。ANOVA残差均方=0.559,MANOVA残差均方=0.018(球形假设误差error(time)sphericity assumed)。个体平均平方和从误差平方和中分离。

1.多变量分析与单变量分析的选择
区别:球形假设
多元方差分析(配对t检验的扩张),不需要进行球形假设。单变量分析(ANOVA的扩展)需要做球形假设(随着时间的发展,结果变量之间具有相等的相关性且方差相等)。球形假设的限制会导致自由度的增加,提高单变量分析的效能。
方法的选择
(1)当样本量小时,效能的提高变得比较重要。样本量N小于重复测量次数*10,不应使用多变量分析,需考虑单变量分析。
(2)先有单变量分析,再有多变量分析。当球形检验不满足时,可以选择多变量分析。但是呢,单变量的分析可以进行校正。所以从原则上讲,球形假设不满足时,两种方法都有可以使用。
(3)只有当两种方法都得到同一结论时,才能真正确认结果变量随时间改变是否显著。当两种方法的结论不一致时,最后的结论需要谨慎考虑。强烈建议采用P值较高的方法。
参考资料:实用流行病学纵向数据分析方法(第2版)