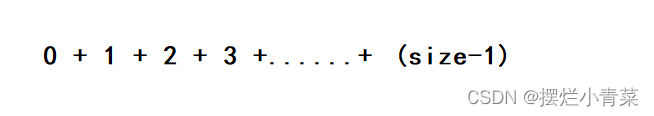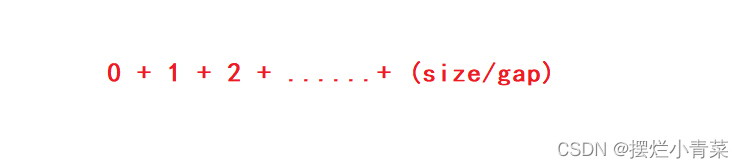深圳幻海软件技术有限公司 欢迎您！
更多

八大排序算法之插入排序+希尔排序

2023-03-15

size end gap
目录一.前言(总体简介)关于插入排序 关于希尔排序:二.插入排序函数首部:算法思路:算法分析插入排序代码实现:插入排序算法的优化前奏: 三.希尔排序(缩小增量排序)1.算法思想: 2.算法拆分解析 序列分组分组预排序:分组预排序的另一种实现方式:希尔排序的实现

目录

一.前言(总体简介)

关于插入排序

 关于希尔排序:

二.插入排序

函数首部:

算法思路:

算法分析

插入排序代码实现:

插入排序算法的优化前奏: 

三.希尔排序(缩小增量排序)

1.算法思想: 

2.算法拆分解析 

序列分组

分组预排序:

分组预排序的另一种实现方式:

希尔排序的实现思路(这里采用Knuth实现法)

关于gap指数式递减的分析:

四.希尔排序的时间复杂度分析

分组预排序的时间复杂度

gap指数式递减过程中,多次分组预排序的总复杂度分析:

经典数据结构书目中对希尔排序复杂度的说明: 

五.实测对比希尔排序与普通插入排序的时间效率

一.前言(总体简介)

关于插入排序

  • 插入排序的思想:将各元素逐个插入到已经有序的序列中的指定位置
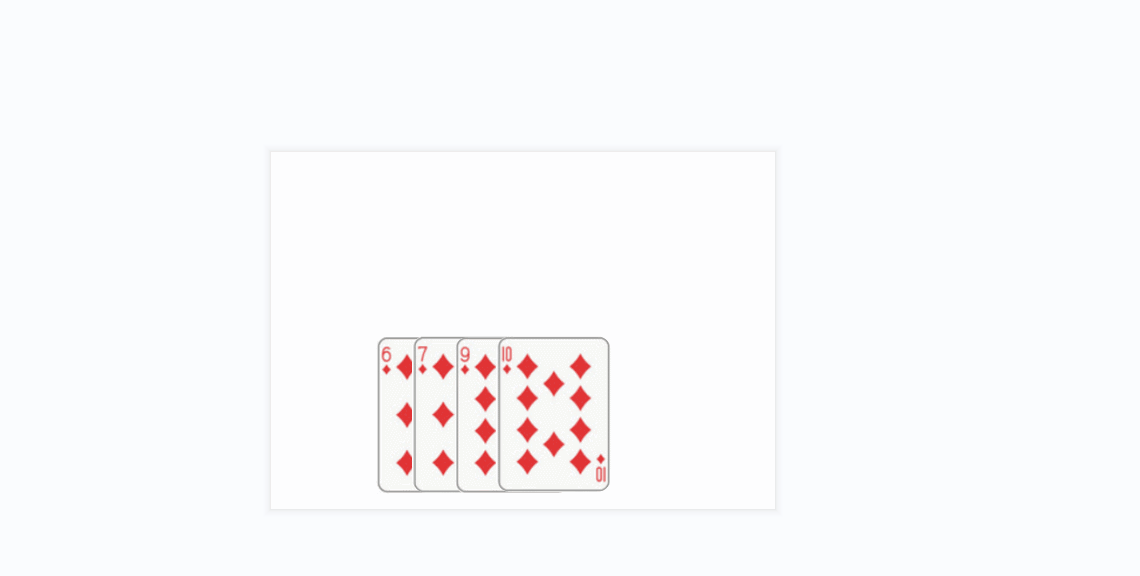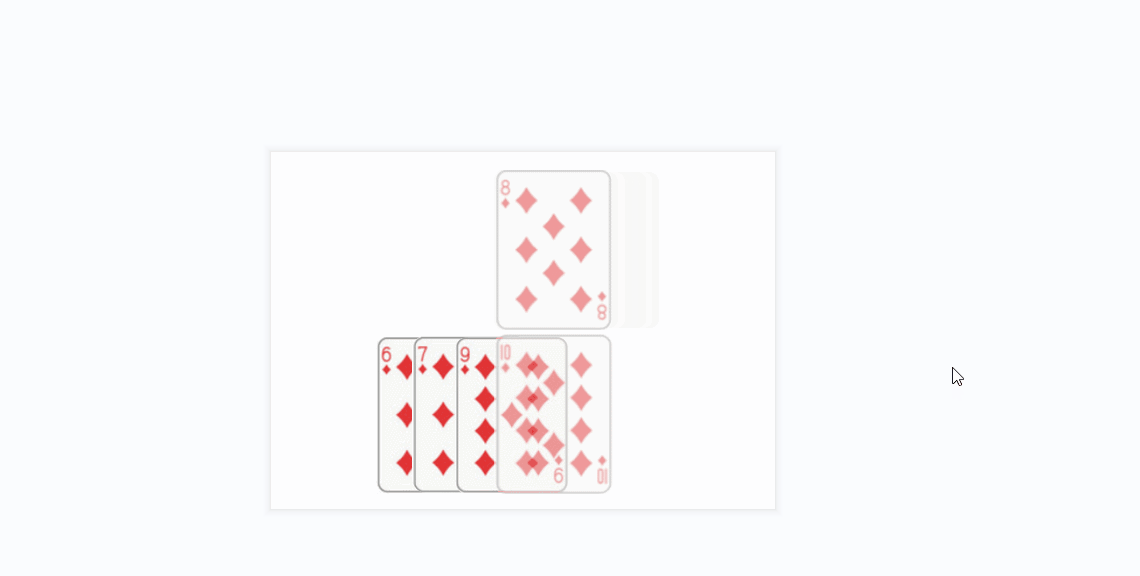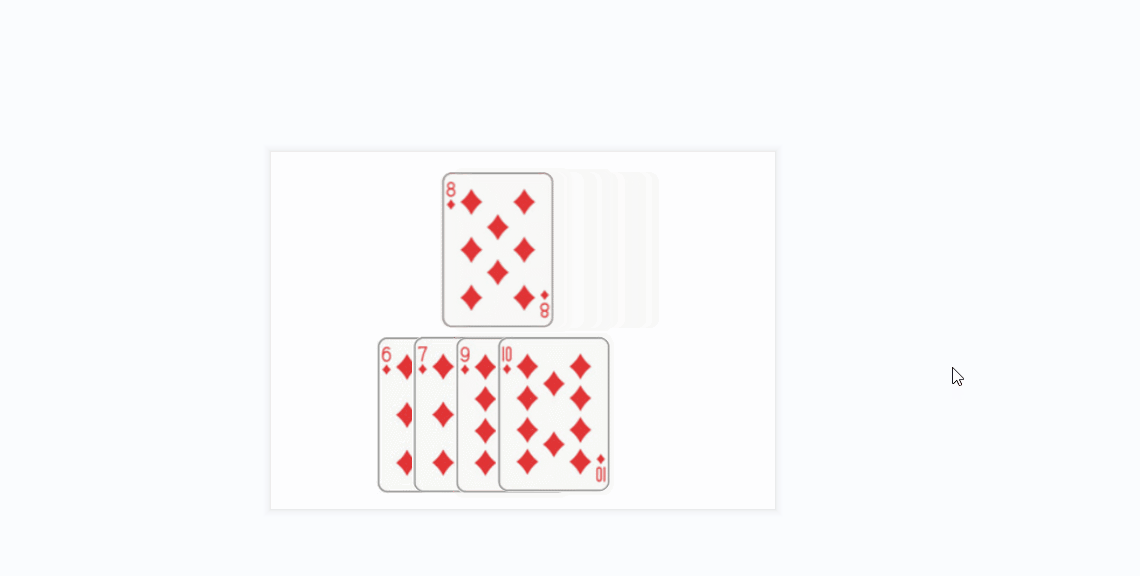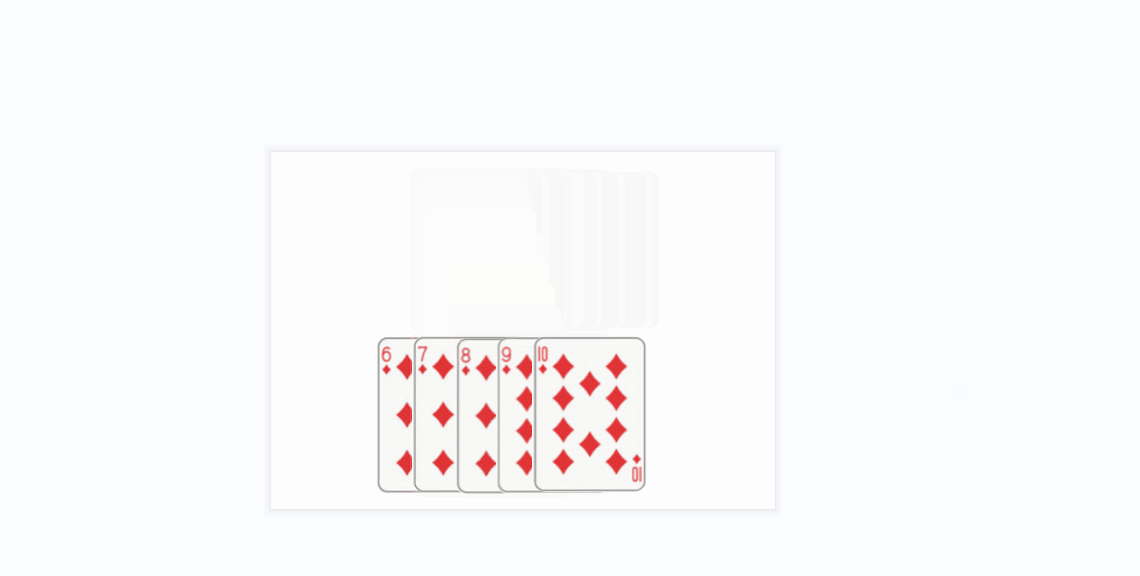
  • 插入排序的思想很类似于我们玩扑克牌时逐张摸牌并整理牌序的方式:
  • 还有一个更贴近算法实现的gif:
  1. 将上面的方条看成数组中的元素
  2. 橙色的方条代表已经排好序的元素序列,蓝色的方条代表待插入的各元素
  3. 在算法实现中,橙色的方条构成的序列用一个下标变量来维护(每次循坏该下标变量加1) 

 关于希尔排序:

  • 希尔排序是插入排序的优化版本,优化算法由希尔本人给出
  • 基本思想是先对数组的子数组(按照一定规则划分而成)进行预排序,使待排序数组变得相对有序,最后再对整个数组进行一次插入排序完成整体的排序

二.插入排序

函数首部:

void InsertSort(DataType* arr, int size);
  • arr是待排序数组首地址指针;
  • size是待排序的元素个数;

算法思路:

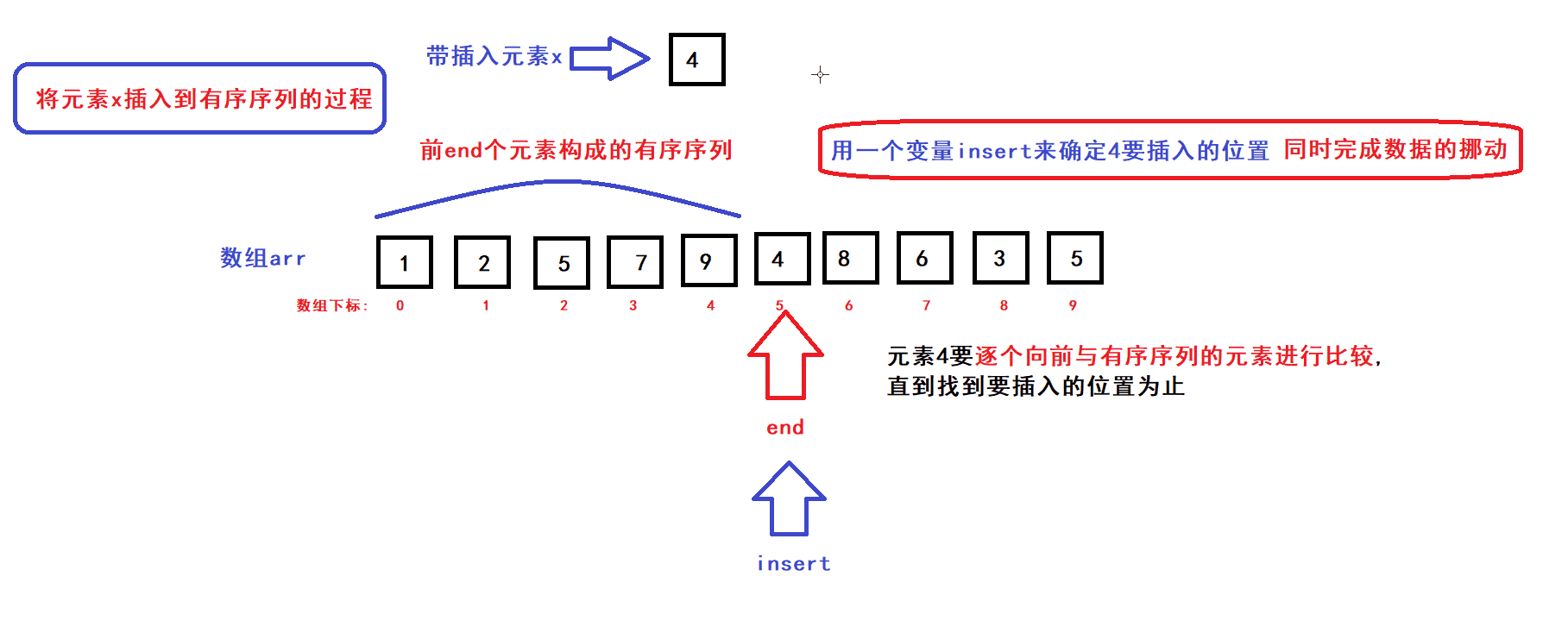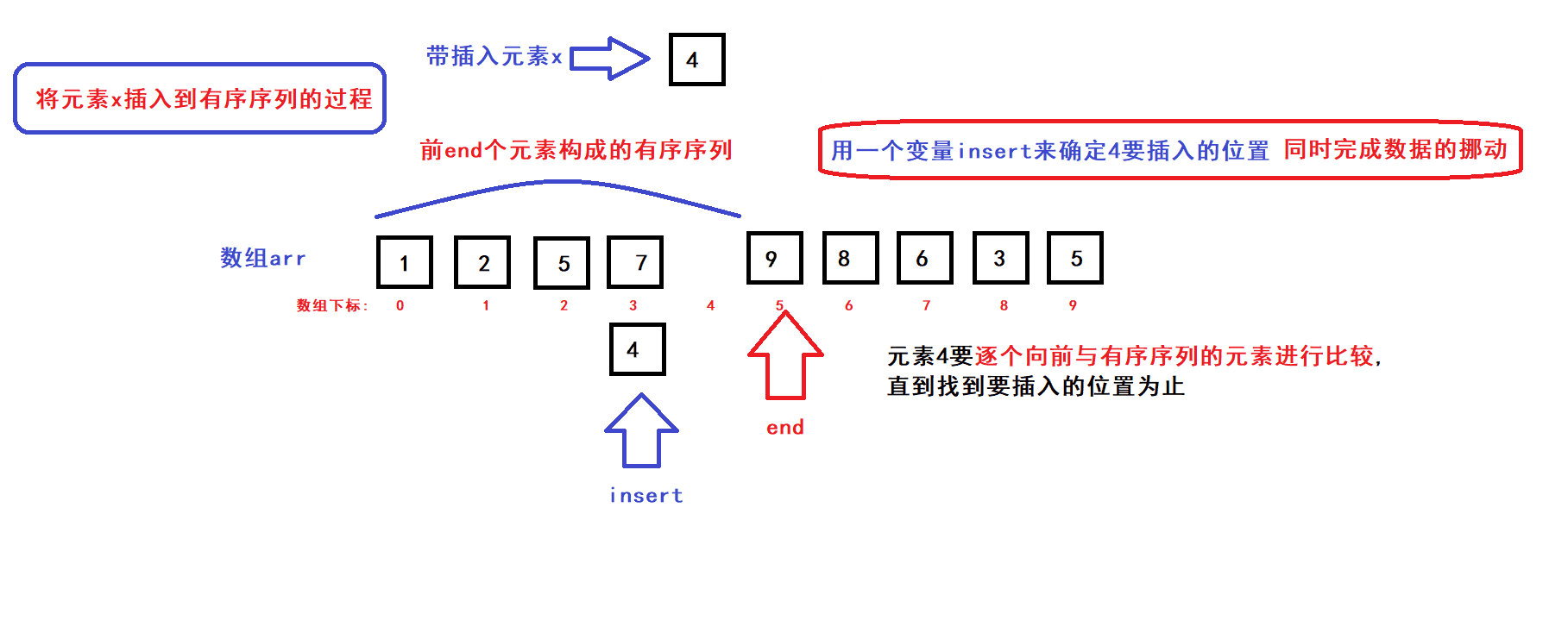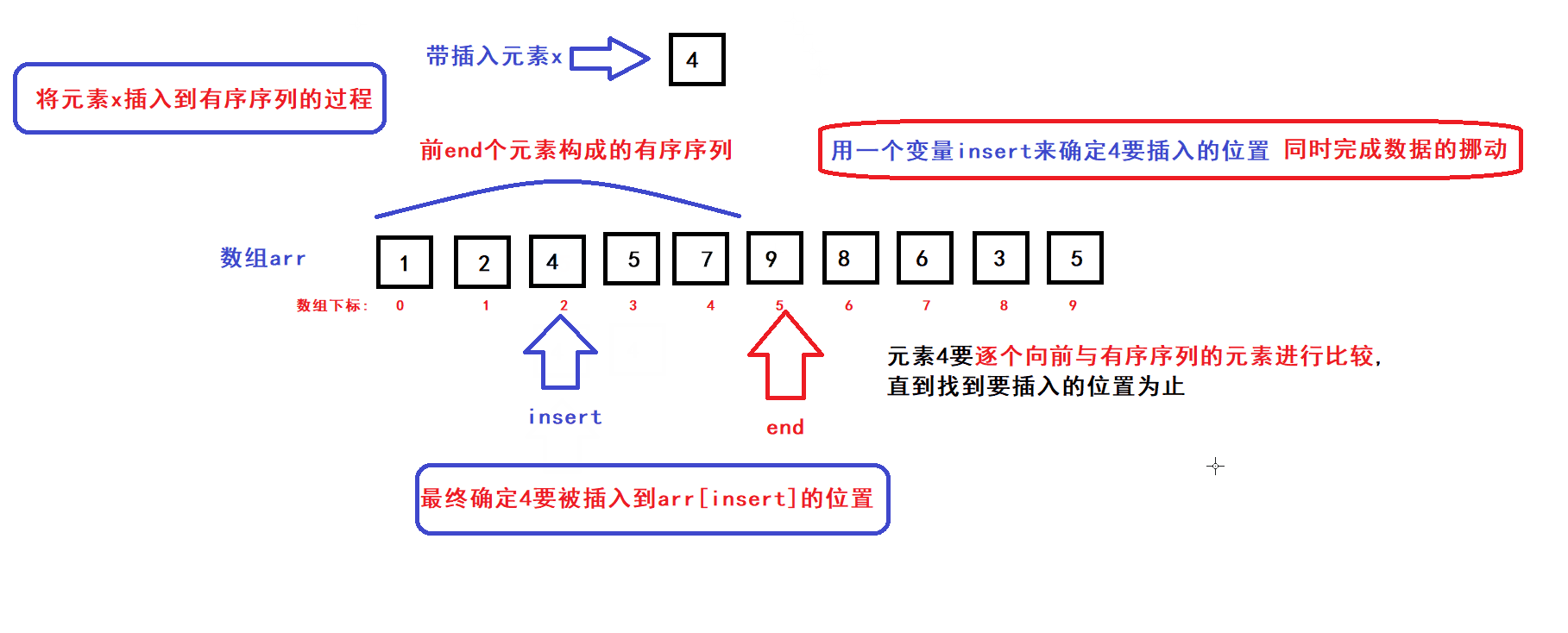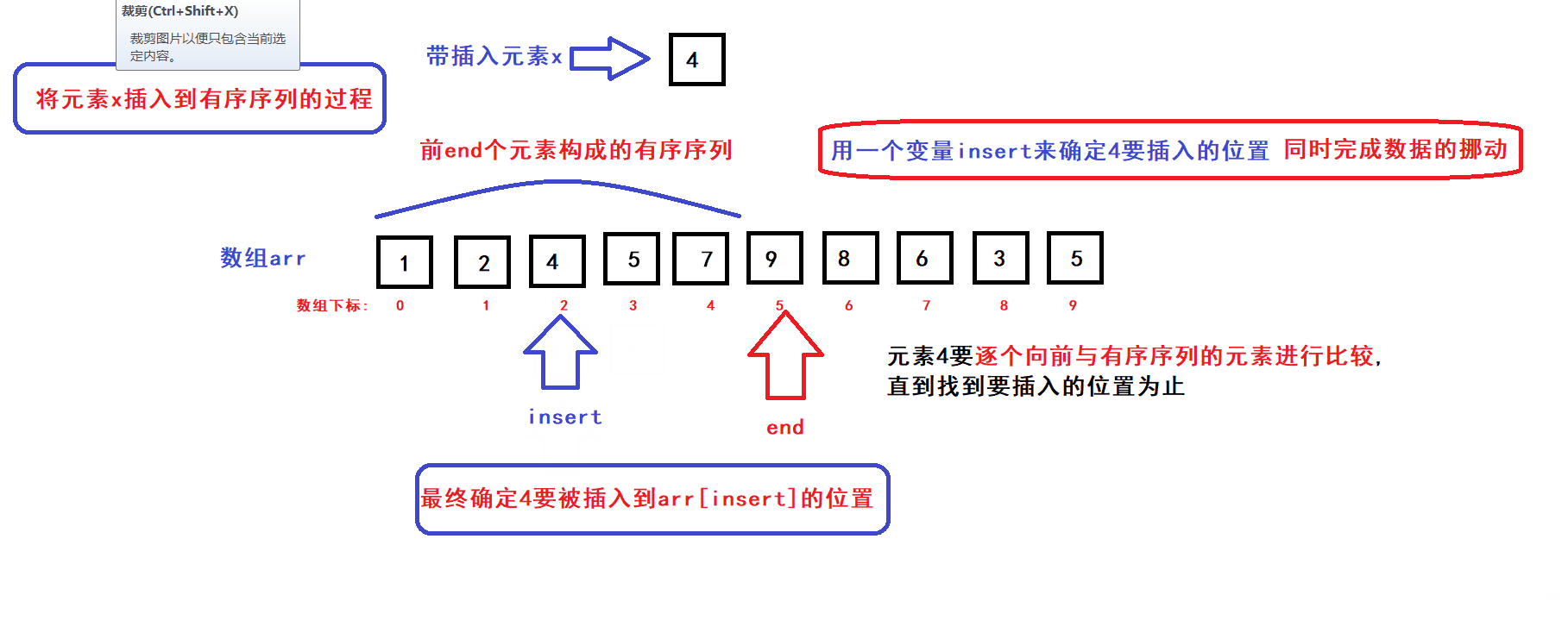
  1. 用一个数组下标变量end来维护前end个有序元素(end初始化为0)
  2. 每个循环过程中,将end下标变量指向的元素插入到前end个元素中的某个指定位置上构成一个end+1个元素的有序序列,然后end加一,接着执行下一次循环直到end遍历完整个数组后循环结束;
  3. 每次循环过程中,x元素插入的位置是通过元素比较来确定的:
  4. end为0时,有序序列元素个数为0;end为1时,有序序列的元素个数为1........;当end为size时,有序序列的元素个数便为size(即数组中size个元素按序排列)此时排序完成
  5. 插入排序便是以这种递推的方式将数组arr调整成有序序列的 

算法分析

  • 从算法思路中可以看到,完成一个元素x插入到前end个元素构成的有序序列的过程中,会发生数据的比较和挪动
  • 在最坏的情况下,每完成一个元素x插入到前end个元素的构成的有序序列的过程中,有序序列的每个元素都要被往后挪动一个位置(即元素比较和挪动的次数为end次)
  • 因此整个排序的过程中发生元素的比较和挪动的总次数为:
  • 所以插入排序的时间复杂度为:O(N^2)  (N为待排序的元素个数);

插入排序代码实现:

两层循环实现:

  • 外层循环用end控制(有size个元素要插入,循环size次)(每次要插入前缀序列的元素x=arr[end])(end下标遍历了整个数组) 
    for(int end =0;end<size;++end)

  • 内层循环用insert控制,用于比较和挪动数据,确定x要插入的位置并完成插入(insert每次从end开始递减直到等于0或者刚好找到x要插入的位置)

  • 以排升序为例:

  1. //以排升序为例
  2. void InsertSort(DataType* arr, int size)
  3. {
  4. assert(arr);
  5. for (int end = 0; end < size; end++)    //用end来维护数组前end个元素构成的有序序列
  6. {
  7. int x = arr[end];//x为待插入有序序列的数据
  8. int insert = end;//用变量insert来确定x要插入的位置
  9. while (insert>0)//通过元素比较确定x要插入的位置
  10. {
  11. if (x < arr[insert-1])   //说明insert不是x要插入的位置
  12. {
  13. arr[insert] = arr[insert-1];   //往后挪动数据为x留出空位
  14. insert--;                      //令insert指向序列前一个元素
  15. }
  16. else
  17. {
  18. break;    //有序序列中x>=arr[insert-1]说明insert是x要插入的位置
  19. }
  20. }//最坏的情况下x会被插入到数组的首地址处(此时数据比较和挪动了end次)
  21. arr[insert] = x;    //完成元素x的插入(继续插入下一个元素)
  22. }
  23. }
  • 注意算法的边界条件:
  1. 外层循环end增加到size时结束循环(数组各元素下标为0到size-1)
  2. 内层循环insert等于0时说明x比前end个元素的有序序列中的所有元素都小,x将被插入到数组下标为insert=0的位置

插入排序算法的优化前奏: 

  • 插入排序算法利用了逐个元素递推插入前缀有序数列的方法完成整个待排序序列的调整(元素插入的过程中,前缀序列有序的性质有时可以大大减少元素的比较和挪动次数).
  • 因此插入排序算法有一个特点:当待排序数组arr整体相对有序时,排序过程的时间复杂度接近O(N),举个例子:
  • 插入排序在处理上图的序列过程中元素总的比较次数为size+2次,元素总的挪动次数为3次(总体上可以认为:在处理整体上大致有序的序列时,插入排序的时间复杂度与size是线性相关的);
  • 插入排序的上述特点为算法的优化提供了可能,如果我们能够在对序列正式进行插入排序之前,让序列整体上变得相对有序,那么就可以降低排序时间复杂度的数量级,这就是希尔排序诞生的思想起点

三.希尔排序(缩小增量排序)

  • 希尔排序算法由大神D.L.Shell于1959年提出而得名,其本质上是在插入排序的基础上进行优化而产生的

先给出排序接口的首部:

void ShellSort(DataType* arr, int size);
  • DataType为typedef定义的元素类型
  • size是待排序数组arr中的元素个数

1.算法思想: 

  • 经过对插入排序的分析我们已经知道:在处理整体上大致有序的序列时,插入排序的时间复杂度与待排序元素个数是线性相关的
  • 因此在正式进行插入排序之前,我们考虑先将序列进行多次分组预排序
  • 多次分组预排序完成后,整体序列将变得相对有序,最后再进行一次插入排序完成整体序列的排序

2.算法拆分解析 

序列分组

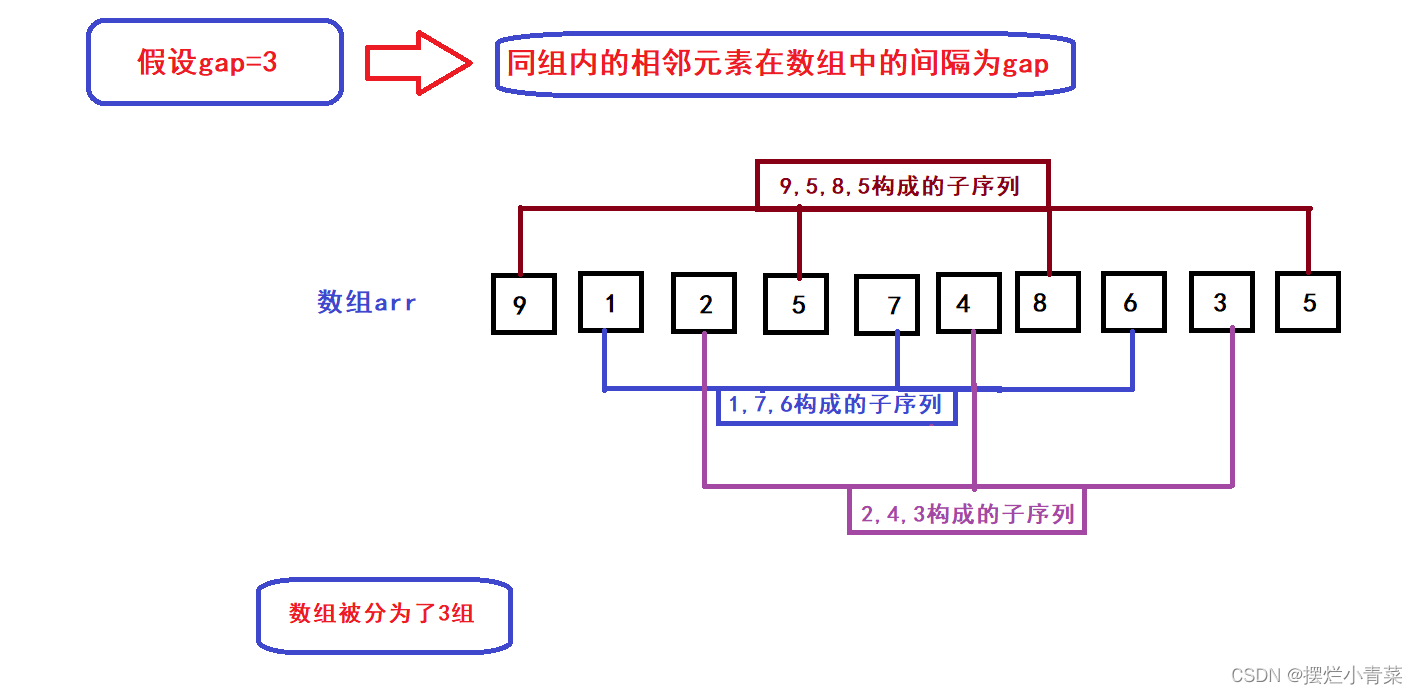
  1. 序列分组方式图文解析:先确定一个gap值(gap<=size)(将序列划分为gap组),从数组第一个元素开始以gap为间隔构成子序列,如图所示:
  2. 根据上述分组方式,我们简单地进行数学上的分析:由于gap<=size,因此我们一定可以将数组arr分为gap个子序列(每个子序列的元素个数至少为(size/gap)个;当size为gap整数倍时,每个子序列的元素个数为(size/gap)个,当size不为gap整数倍时,每个子序列元素个数最大为(size/gap)+1个);(以上数学表达式中的除法皆为向下取整除法)
  3. 我给这种序列分组模式取个名字:序列固定间隔分组法
  4. 序列固定间隔分组法的另外一种图示形式:
  • 可见每个子序列的首元素分别为下标为0到gap-1的元素
  • 完成了序列的固定间隔分组后,接下来就要对这些子序列分别进行插入排序,即分组预排序

分组预排序:

  • 确定了gap值后,对各个子序列分别进行插入排序:(图示中以gap=3为例子)
  • 分组预排序的代码实现思路:(最基础的思路是三层循环实现)
  1. 数组arr被分为gap组, 所以要对gap个子序列进行插入排序即最外层循环gap次,最外层循环用start变量来控制(初始化为0),边界条件为start<gap;
  2. 内两层循环的代码架构与插入排序完全一致
  • 分组预排序的代码实现(建立在插入排序代码的框架上):
    1. void ShellSort(DataType* arr, int size)
    2. {
    3. assert(arr);
    4.  
    5. int gap;//将数组划分为gap组(gap待定)
    6. for (int start = 0; start < gap; ++start)   //start为每个子序列的首元素下标(gap个子序列循环gap次)
    7. {
    8. for (int end = start; end < size; end += gap)//用end来维护子序列中的前缀有序序列(end不能大于或等于size)(end下标遍历了子序列)
    9. {
    10. int x = arr[end];//x为待插入前缀有序序列的元素
    11. int insert = end;//用insert确定x要插入的位置
    12. while (insert>start)//insert=start时说明x要插入到子序列首元素的位置
    13. {
    14. if (x < arr[insert - gap])//说明insert不是x要插入的位置
    15. {
    16. arr[insert] = arr[insert - gap];    //挪动数据,为x空出位置
    17. insert -= gap;//指向子序列的前一个元素
    18. }
    19. else                                    //x >= arr[insert - gap]说明insert就是x要插入的位置
    20. { 
    21. break;
    22. }
    23. }
    24. arr[insert] = x;//完成x元素的插入
    25. }
    26. }
    27. }

  • 代码段完成了一次分组预排序(分组间隔为gap)

  • 代码段中如果gap等于1,分组预排序则变为普通的插入排序 

分组预排序的另一种实现方式:

  • 分组预排序可以用两层循坏来实现:

  • 注:两层循环的分组预排序和三层循环的分组预排序其实本质上没有区别,只是元素调整顺序不一样(三层循环是一组接一组子序列完成插入排序,两层循环是逐个元素完成调整)

    1. void ShellSort(DataType* arr, int size)
    2. {
    3. assert(arr);
    4. int gap;//gap值待定
    5. for (int end = 0; end < size; ++end)    //用end来遍历数组每一个元素
    6. {
    7. int x = arr[end];//x为待插入子序列前缀的元素
    8. int insert = end;//用insert确定x要插入的位置
    9. while (insert >= gap)//insert<gap的时,insert为下标的元素不需要调整
    10. {
    11. if (x < arr[insert - gap])//说明insert不是x要插入的位置
    12. {
    13. arr[insert] = arr[insert - gap];    //挪动数据,为x空出位置
    14. insert -= gap;//指向子序列的前一个元素
    15. }
    16. else                                    //x >= arr[insert - gap]说明insert就是x要插入的位置
    17. {
    18. break;
    19. }
    20. }
    21. arr[insert] = x;//完成x元素的插入
    22. }
    23. }

    三层循环改为两层循环,其具体代码思路图解如下:

  • 三层循环的写法和两层循环的写法本质都是完成了gap为某确定值时的一次分组预排序

  • 同样地,代码段中如果gap等于1,分组预排序则变为普通的插入排序 

  • 后续为了简洁起见,我们采用两层循环的分组预排序实现法来完成希尔排序

希尔排序的实现思路(这里采用Knuth实现法)

  • 由之前的分析我们可以知道:gap的值确定了序列的一个划分(序列被划分为gap个子序列),对这些子序列分别进行插入排序便完成了一次序列的分组预排序
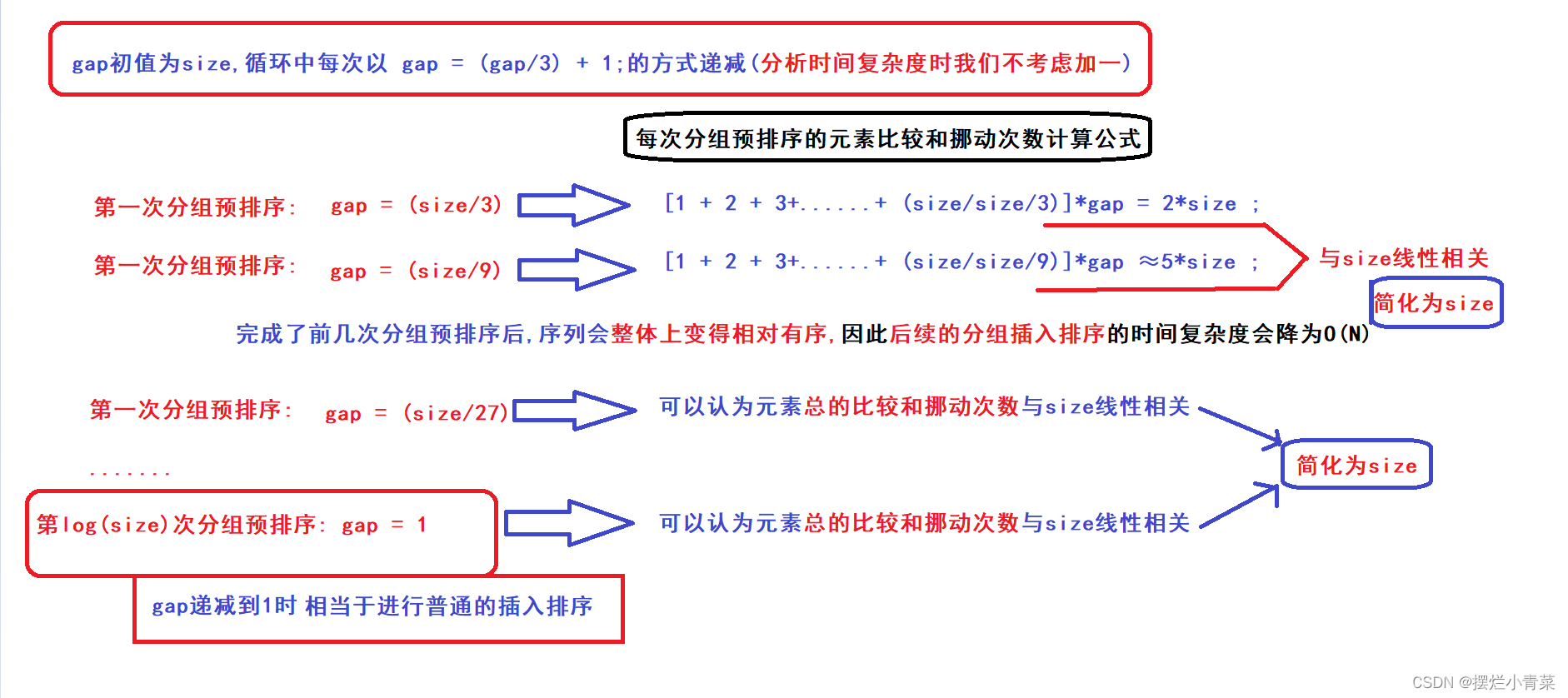
  • 我们置gap的初始值为size,gap每次循环按照gap = (gap/3)+1的方式递减(由简单的数学分析可知gap一定会减小到1)(加1就是为了保证gap最终一定会减小到1)
  • 对于每一个gap值我们都对待排序数组进行一次分组预排序
  • 当gap减小到1时,数组已经经过了一次或多次分组预排序,最后再完成一次gap为1的分组预排序(gap为1时的分组预排序等价于普通的插入排序)从而完成数组整体的排序(gap为1的排序必须进行,否则不能保证整体序列一定有序)
  • 我们只需在分组预排序的实现代码外层再套一层由gap控制的循环即可实现上述过程: 
    1. void ShellSort(DataType* arr, int size)
    2. {
    3. assert(arr);
    4. int gap = size;
    5. while (gap>1)                  //gap为1时序列已经完成了普通插入排序,排序完成
    6. {
    7.         gap = gap/3 + 1;           //缩小gap的值
    8. for (int end = 0; end < size; ++end)    //用end来遍历数组每一个元素
    9. {
    10. int x = arr[end];//x为待插入子序列前缀的元素
    11. int insert = end;//用insert确定x要插入的位置
    12. while (insert >= gap)//insert<gap的时,insert为下标的元素不需要调整
    13. {
    14. if (x < arr[insert - gap])//说明insert不是x要插入的位置
    15. {
    16. arr[insert] = arr[insert - gap];    //挪动数据,为x空出位置
    17. insert -= gap;//指向子序列的前一个元素
    18. }
    19. else                                    //x >= arr[insert - gap]说明insert就是x要插入的位置
    20. {
    21. break;
    22. }
    23. }
    24. arr[insert] = x;//完成x元素的插入
    25. }
    26. }
    27. }

关于gap指数式递减的分析:

  • 希尔排序算法中,gap从size开始呈指数式递减. (这也是缩小增量排序这个名字的来源)
  • 因此,算法中分组预排序的执行次数的数量级为(logN) (N=size)
  • gap设计成指数式递减这一思想非常重要,这样既保证了在进行gap=1的插入排序之前,完成了一定次数的分组预排序,又保证了分组预排序的次数不会太多(分组预排序的次数如果太多反倒会降低算法整体的效率)

四.希尔排序的时间复杂度分析

希尔排序接口首部:

void ShellSort(DataType* arr, int size)

分组预排序的时间复杂度

序列分组图示:

  • 为了方便分析,我们假设每次分组预排序,size都为gap的整数倍:根据序列固定间隔分组法,待排序数组被划分为gap个子序列,每个子序列元素个数为(size/gap)个
  • 根据插入排序的时间复杂度计算公式:完成每组子序列的插入排序算法循环中元素比较和挪动的总次数的数量级为:
  • 即完成一次分组预排序的时间复杂度计算表达式为:

gap指数式递减过程中,多次分组预排序的总复杂度分析:

  • 可以发现一个规律:gap值越大(gap<=size)的分组预排序元素比较和挪动次数的上限就越低(复杂度越接近线性),因此利用较大的gap值进行分组预排序将总体序列调整为相对有序序列的设计非常巧妙！！！

  • 将size写成N,则希尔排序的时间复杂度总体的数量级大致为NlogN
  • 该证明并不严格,但是总体上反映出了希尔排序通过多次分组预排序的方法尝试降低整体排序的时间复杂度数量级的思想。
  • 希尔大神设计该算法时,gap的递减方式是:gap=gap/2；
  • gap = (gap/3)+1这种缩小增量的公式是由kunth大神给出的,希尔排序的最优gap递减公式目前尚未求得(这牵涉到一些尚未得到完全解决的数学难题)

经典数据结构书目中对希尔排序复杂度的说明: 

以下文段摘自《数据结构-用面相对象方法与C++描述》--- 殷人昆

  • gap的取法有多种.最初Shell提出取gap=gap/2,直到gap=1,后来Kunth提出取gap=(gap/3) +1.还有人提出都取奇数为好,也有人提出各gap互质为好.无论哪一种主张都没有得到证明。
  • 对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算关键码的比较次数和对象移动次数,但想要弄清关键码比较次数和对象移动次数与增量选择之间的依赖关系,并给出完全的数学分析,还没有人能够做到。在Kunth所著的《计算机程序设计技巧》第三卷中,利用大量的实验数据统计资料得出,当n很大时,关键码平均比较次数和对象平均移动次数大约在n^1.25 到1.6n^1.25范围内,这是在利用直接插入排序作为子序列排序方法的情况下得到的

从上述文段中我们可以得知,受当前数学分析的限制,我们可以暂且根据Kunth大神的实验结果,将希尔排序的时间复杂度看成是: O(N^1.25)

五.实测对比希尔排序与普通插入排序的时间效率

  • 利用随机数生成器创建两个十万个元素的相同整形数组,一个用直接插入排序进行排序,另外一个用希尔排序进行排序,打印出两者所消耗的时间(单位为毫秒) 
    1. int main()
    2. {
    3. srand(time(0));
    4. const int N = 100000;
    5. int* arr1 = (int*)malloc(sizeof(int) * N);
    6. int* arr2 = (int*)malloc(sizeof(int) * N);
    7. for (int i = 0; i < N; ++i)
    8. {
    9. arr1[i] = rand();
    10. arr2[i] = arr1[i];
    11. }
    12. int begin1 = clock();
    13. InsertSort(arr1, N);
    14. int end1 = clock();
    15. printf("IsertSort:%d\n", end1-begin1);
    16.  
    17.  
    18. int begin2 = clock();
    19. ShellSort(arr2, N);
    20. int end2 = clock();
    21. printf("ShellSort:%d\n", end2-begin2);
    22. return 0;
    23. }

  • 可见希尔排序的算法优化思路虽然新奇复杂,但毫无疑问的是,希尔大神对插入排序所进行的优化是非常成功的！！！！(而且数据量越大希尔排序的优化效果就越明显)

文章知识点与官方知识档案匹配，可进一步学习相关知识
算法技能树首页概览40493 人正在系统学习中
【算法系列篇】滑动窗口
走进人工智能|深度学习 算法的创世纪