目录

【实验目标】

【实验内容】

【代码要求】

【文档要求】

【实验目标】

1. 理解前向传播和反向传播
2. 应用作业一中提到的基本操作

【实验内容】

假设X有n个样本，属于m=3个类别, 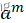表示样本属于第m类的概率，请实现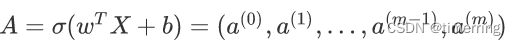的三次前向传播及反向传播(更新参数ω和b)，每次反向传播结束后更新并输出参数ω和b的值，计算cross entropy loss，其中σ(∙)表示sigmoid函数。

【代码要求】

按代码模板实现函数功能

【文档要求】

前向传播及反向传播涉及到的公式计算（参考）

①在前向传播的过程中，可以如下表示

 粘贴代码输出结果截图。

import os  
import numpy as np  
import math  
  
  
def sigmoid(x):  
    """ 
    Compute the sigmoid of x 
 
    Arguments: 
    x -- A scalar or numpy array of any size 
 
    Return: 
    s -- sigmoid(x) 
    """  
    # write your code here  
    sig = 1 / (1 + np.exp(-x))  
    return sig  
  
  
def softmax(x):  
    """Calculates the softmax for the input x. 
 
    Argument: 
    x -- A numpy matrix of shape (n,) 
 
    Returns: 
    s -- A numpy matrix equal to the softmax of x, of shape (n,) 
    """  
    # write your code here  
    x = np.exp(x) / np.sum(np.exp(x), axis=0, keepdims=True)  
    return x  
  
  
def cross_entropy_loss(target, prediction):  
    """ 
    Compute the cross entropy loss between target and prediction 
 
    Arguments: 
    target -- the real label, a scalar or numpy array size = (n,) 
    prediction -- the output of model,  a scalar or numpy array, size=(n, c) 
 
    Return: 
    mean loss -- cross_entropy_loss(target, prediction) 
    """  
    # write your code here  
    delta = 1e-6  
    return -np.sum(prediction * np.log(target + delta))  
  
  
def forward(w, b, x):  
    """ 
    Arguments: 
    w -- weights, a numpy array of size (m, 1) 
    b -- bias, a scalar 
    x -- data of size (n, m) 
 
    Return: 
    prediction 
    """  
    ## write your code here  
    prediction = sigmoid(x @ w + b)  
    # print(prediction.shape)  
    return prediction  
  
  
def backward(x, target, prediction):  
    """ 
    Arguments: 
    x -- data of size (n, m) 
    target -- data of size (n, num_class) 
    prediction -- data of size (n, num_class) 
 
    Return: 
    dw, db 
    """  
    delta = target - prediction  
    db = delta  
    dw = sigmoid(x.T) @ delta  
    return dw, db  
  
  
# don't edit  
if __name__ == '__main__':  
    ## three samples  
    x = np.array([[12, 3, 7, 4], [3, 10, 4, 9], [9, 6, 2, 0]])  
    target = np.array([0, 1, 2])  
    num_class = 3  
    ## learning rate of the gradient descent update rule  
    learning_rate = 0.001  
    ## one-hot label  
    target = np.eye(num_class)[target]  
    n, m = x.shape  
    w = np.zeros([m, num_class])  
    b = 0  
    # three iterations of forward and backward  
    for i in range(3):  
        prediction = forward(w, b, x)  
        loss = cross_entropy_loss(target, softmax(prediction))  
        dw, db = backward(x, target, prediction)  
        # update w and b  
        w = w - learning_rate * dw  
        b = b - learning_rate * db  
        print("iter = {}, w = {}, b = {}, loss= {}".format(i, w, b, loss))  

初次的实验结果如下：

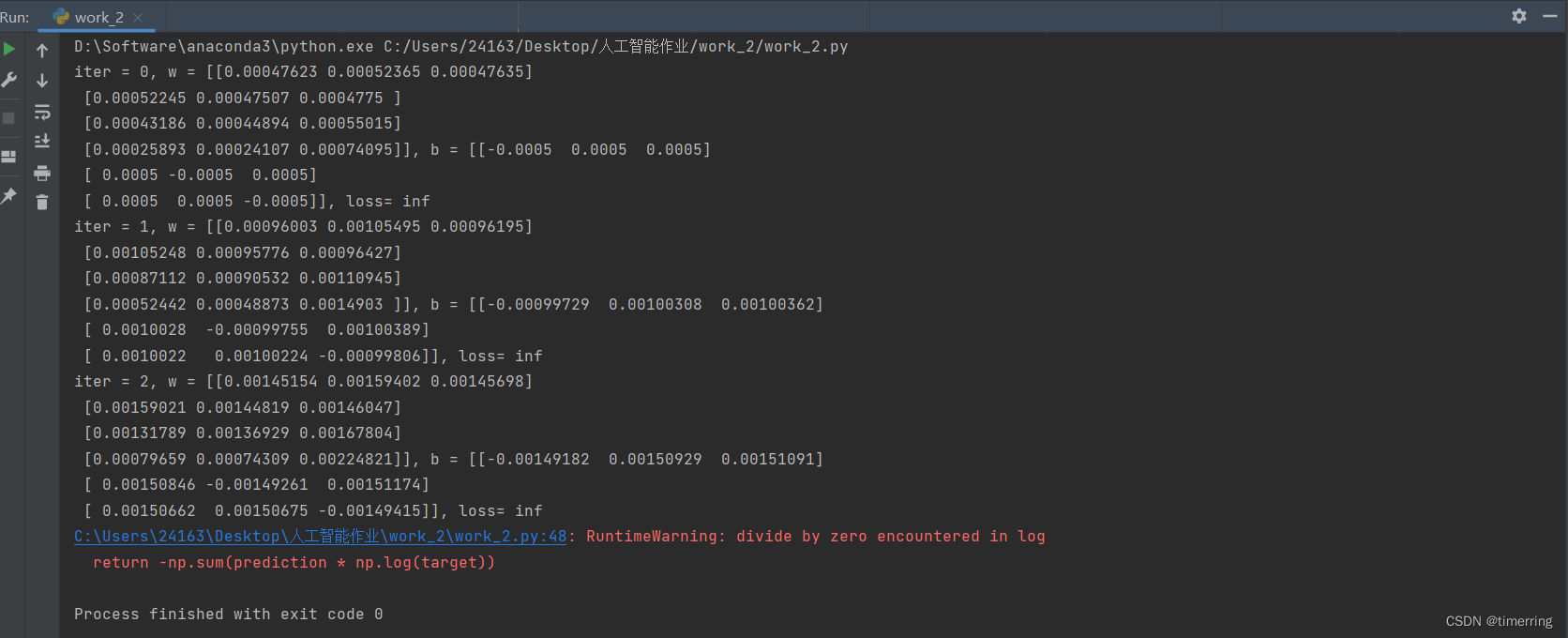
        可见按照定义写出函数时结果并不理想，因为在main代码中设置的参数权重都设置为0了，导致log以后数值无穷，导致内存溢出，且一般这样做的效果并不好，在Andrew Ng的DL课程中有对应的解释。

        把权重或者参数都初始化为0，那么梯度下降将不会起作用。把权重都初始化为0，那么由于隐含单元开始计算同一个函数，所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同的，即隐含单元仍是对称的。这个问题的解决方法就是随机初始化参数。把𝑊设为np.random.randn（m, num_class） (生成高斯分布)，通常再乘上一个小的数，比如0.01，这样把它初始化为很小的随机数，只要随机初始化𝑊你就有不同的隐含单元计算不同的东西，因此不会有symmetry breaking 问题了。

        由于不能修改main中的初始化代码，因此我在网上查找了对应的解决方法，发现可以通过对数据精度的处理解决这个问题，这里我通过添加delta量，改变了浮点数的精度为1e-6，计算效果良好。如下所示：

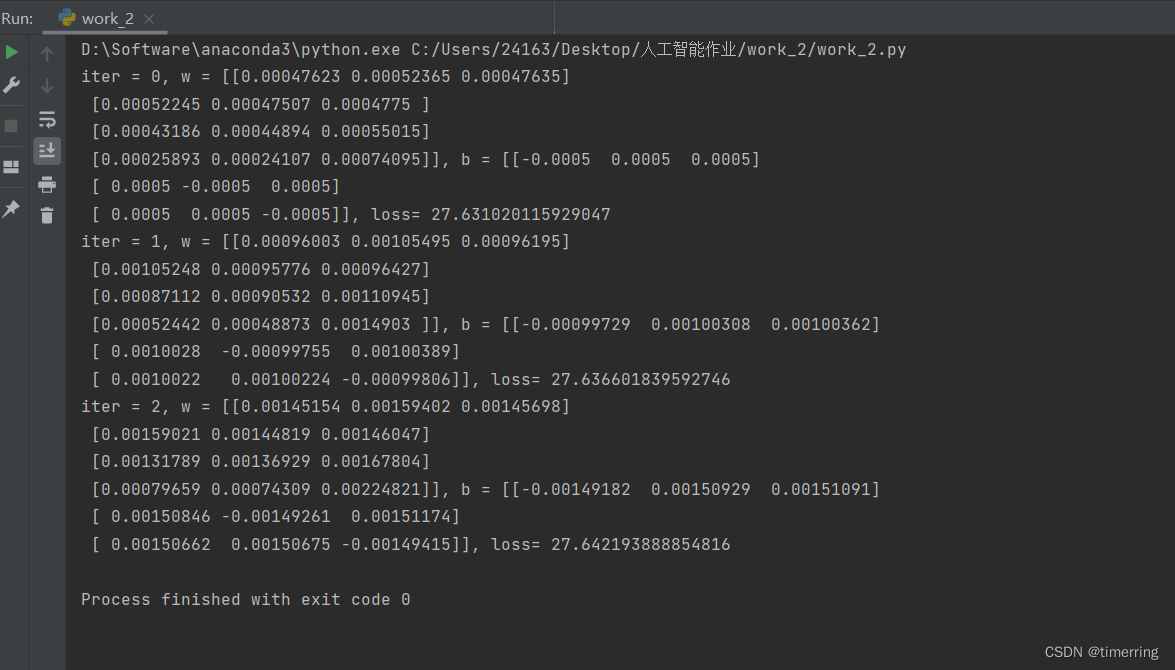
初学人工智能导论，可能存在错误之处，还请各位不吝赐教。

受于文本原因，本文相关实验工程无法展示出来，现已将资源上传，可自行下载。

山东大学人工智能导论实验2工程文件-前向传播和反向传播-深度学习文档类资源-CSDN下载山东大学人工智能导论实验2工程文件-前向传播和反向传播详解博客地址：https://blog.cs更多下载资源、学习资料请访问CSDN下载频道.https://download.csdn.net/download/m0_52316372/85912862